- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
پارسا میخواهد در آزمون مرحله یک المپیاد شرکت کند. او در آزمونها به استراتژی ثابتی پایبند است: سؤالها را به ترتیب از $1$ تا $n$ بررسی میکند، هر سؤالی که حل شود را همانجا علامت میزند و به سؤال بعدی میرود. او هرگز به عقب برنمیگردد و هیچ سؤالی را دوبار پاسخ نمیدهد. در یک آزمون تمرینی، پارسا برخی سؤالها را نتوانسته حل کند و آنها را خالی گذاشته است.
او در کل به $m$ سوال در پاسخبرگ پاسخ داده است. $i$-امین سوالی که به آن پاسخ داده است، سوال $p_i$ است که برای آن گزینهی $c_i$ را در پاسخبرگ وارد کرده است.
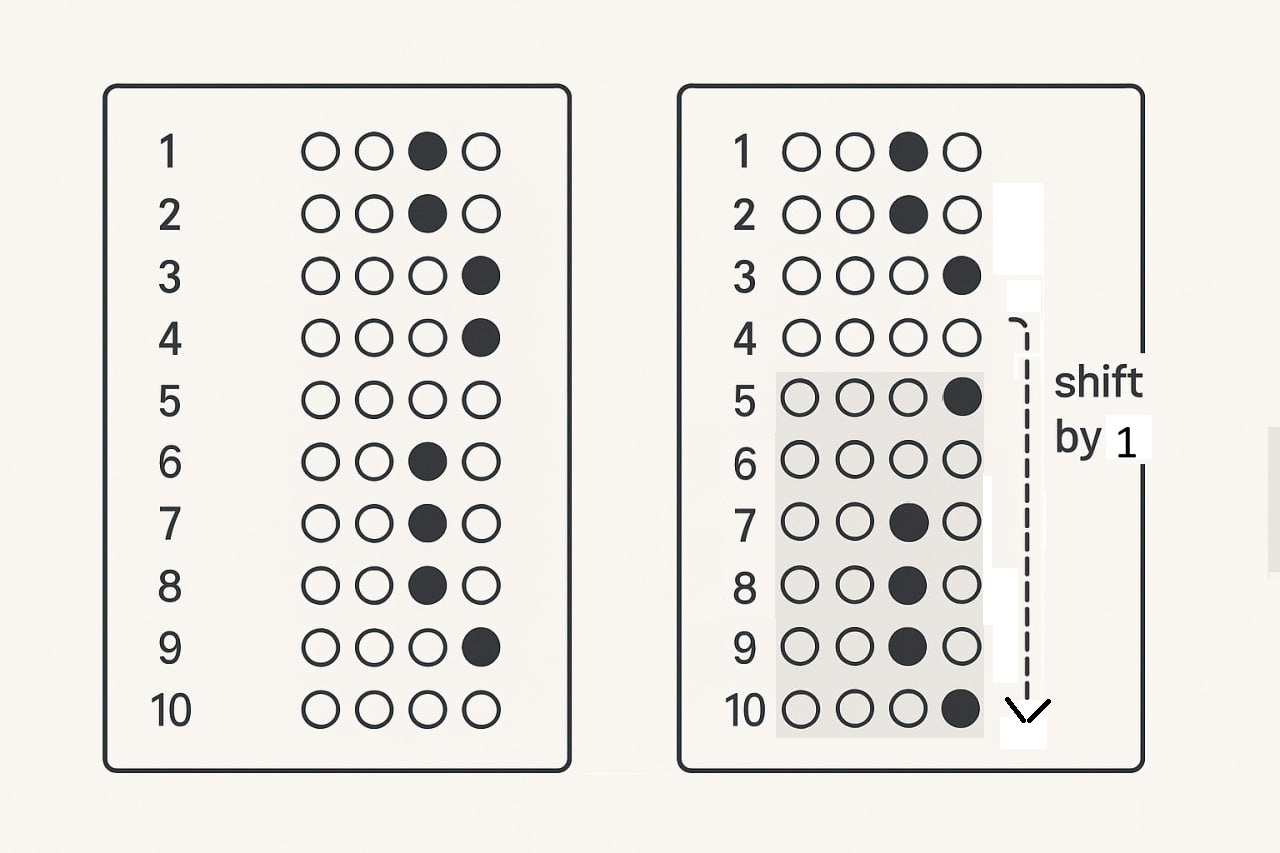
پارسا گمان میکند حداکثر یکبار در وارد کردن شماره سؤالها روی پاسخبرگ اشتباه کرده است. تعریف دقیق یکبار اشتباه چنین است: در یک بازه متوالی از پاسخ ها برای سوالات، برای هر سوال شماره سؤالی که پارسا برای آن پاسخ را ثبت کرده به اندازه عدد صحیح غیرصفر $d$ جابهجا شده است؛ یعنی پاسخهای آن بازه بهجای سؤالهای ${p_\ell,\dots,p_r}$ روی سؤالهای ${p_\ell+d,\dots,p_r+d}$ ثبت شدهاند (یا برعکس، معادل با اینکه «سؤالات مقصود» او در آن بازه ${p_i-d}$ بودهاند). خارج از این بازه، هیچ جابهجایی رخ نداده است. این اشتباه بیش از یکبار رخ نداده یا ممکن است اصلاً رخ نداده باشد.
توجه کنید که پارسا پاسخها را به ترتیب و بدون تکرار وارد کرده است؛ بنابراین دنباله «سؤالات پاسخ داده شده» باید صعودی و در بازهٔ $[1..n]$ باشد و هیچ سؤالی دوبار پاسخ داده نشده باشد.
شما پاسخ برگ را دارید و معلوم نیست که کجا و به چه شکلی اشتباه انجام شده. هدف شما این است که با فرض امکان وقوع «حداکثر یکبار اشتباه» به شکل فوق، بیشترین نمره ای که پارسا با درست وارد کردن سوالات میتوانست بدست بیاورد(تعداد پاسخهای درست نسبت به کلید آزمون) را محاسبه کنید.
ورودی
در خط اول ورودی عدد $T$ (تعداد تستها) آمده است. سپس برای هر تست:
- خط اول شامل دو عدد صحیح $n$ و $m$ است؛ بهترتیب تعداد کل سؤالها و تعداد سؤالهایی که پارسا پاسخی برای آنها وارد کرده است.
- خط دوم رشتهای $S$ با طول $n$ شامل حروف
AتاEاست که کلید صحیح آزمون را نشان میدهد؛ $S[i]$ پاسخ صحیح سؤال $i$ام است. - سپس $m$ خط میآید؛ در هر خط یک عدد صحیح $p_i$ $(1 \le p_i \le n)$ و یک حرف $c_i \in {A,B,C,D,E}$ آمده است. اینها بیان میکنند پارسا روی پاسخبرگ برای سؤال $p_i$ گزینهٔ $c_i$ را علامت زده است.
- تضمین میشود $p_1 < p_2 < \dots < p_m\ $.
خروجی
برای هر تست، یک خط شامل یک عدد چاپ کنید: بیشترین تعداد پاسخهای درست که میتوان برای پارسا فرض کرد.
محدودیتها
$$ 1 \le T \le 10^4 $$ $$ 1 \le n \le 5000,\quad 0 \le m \le n $$ $$ \sum n \le 5000 $$
مثالها
ورودی نمونه ۱
4
5 4
AECDB
1 A
2 A
4 C
5 B
7 2
AAACDAA
1 C
3 D
7 2
AAACDAA
1 C
2 D
10 5
ABECCDBAEA
3 B
4 E
6 C
8 A
10 E
خروجی نمونه ۱
3
1
2
4
ارسال پاسخ برای این سؤال