• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

در پایان شهریور خونین بالاخره تکلیف کاراکتر اصلی ۱ روشن شد و او چشم از جهان بست تا دیگر کسی نتواند کاراکترهای کمکی بی گناه را اذیت کند. اما از آنجایی که داستان این کانتست بسیار غم انگیز می‌شود اگر کاراکتر اصلی ۱ تنها و بی‌کس و در میان انبوهی از کاراکترهای کمکی بمیرد، پس یک کاراکتر اصلی ۰ای پیدا می‌شود که از قضا در زمانی که کاراکتر اصلی ۱ خودش هم کاراکتر کمکی بوده، معلمش بوده است. در این لحظات آخر زندگی برای کاراکتر اصلی ۱، کاراکتر اصلی ۰ سر او را روی پاهایش می‌گذارد و می‌خواهد کاری کند که او در هنگام مرگش با رضایت و شادکامی از دنیا برود، به همین دلیل در $q$ ثانیه‌ی آخر زندگی کاراکتر اصلی ۱، $q$ سوال از او می‌پرسد:

سوال او بی‌ربط به فضای اطراف آن‌ها در این لحظات نیست، درختی در حیاط مدرسه وجود دارد که رئوسش شماره‌گذاری شده‌اند و ریشه‌دار است و ریشه‌ی آن راس ۱ است. کاراکتر اصلی ۰ در هر ثانیه شماره‌ی دوتا از رئوس این درخت را به کاراکتر اصلی ۱ می‌دهد و چون در لحظات مرگ کمی از بنیه‌ی علمی و توان کاراکتر اصلی ۱ کم شده است تضمین می‌کند که راس دومی که داده است حتما در زیردرخت راس اول است. به عبارت دیگر $ v$ و $u$ را می‌دهد که $ u$ در زیردرخت $v$ است. چیزی که کاراکتر اصلی ۱ باید بگوید این است که طول بزرگترین مسیر در زیردرخت $v$ با شروع از $u$ چقدر است به عبارت دیگر اگر بقیه‌ی درخت به غیر از زیردرخت راس $v$ حذف شود، بلندترین مسیری که یک راس آن $u$ باشد چه طولی دارد.

کاراکتر اصلی ۱ دانا که تمام این اتفاقات را از قبل پیش بینی می‌کرده است دستگاهی ساخته و با خود همراه دارد که جواب تمام این سوالات کاراکتر اصلی ۰ را بدهد تا او فکر کند که کاراکتر اصلی ۱ با شادی از دنیا رفته است.

برنامه‌ای بنویسید که مانند دستگاه کاراکتر اصلی ۱ عمل کند و به سوالات کاراکتر اصلی ۰ پاسخ دهد.

ورودی

در خط اول ورودی دو عدد طبیعی $n$ و $q$ داده می‌شوند.

در خط بعدی $n - 1$ عدد که $i$امین عدد نشان‌دهنده‌ی شماره‌ی راس پدر راس $i + 1$ است.

در $q$ خط بعدی $q$ پرسش مطرح می‌شوند، در هر خط دو عدد $v$ و $u$ را می‌دهد.

$$1 \leq n \leq 100 \ 000$$ $$1 \leq q \leq 100 \ 000$$ $$1 \leq v, u \leq n$$

خروجی

در $q$ خط پاسخ $q$ پرسش مطرح شده را بدهید.

مثال

ورودی نمونه

7 3
1 1 2 2 3 3
1 5
2 5
7 7

خروجی نمونه

4
2
0

توضیح

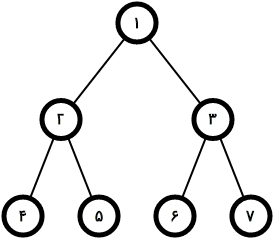
در ثانیه‌ی اول، کاراکتر اصلی ۱ باید بلندترین مسیر با شروع از راس ۵ در کل درخت رو بگوید (زیردرخت ریشه، کل درخت را شامل می‌شود) که بلندترین مسیر با شروع از راس ۵، مسیر ۵ ۲ ۱ ۳ ۶ یا ۵ ۲ ۱ ۳ ۷ می باشند که طولشان ۴ است.

در ثانیه‌ی دوم، کاراکتر اصلی ۱ باید بلندترین مسیر با شروع از راس ۵ در زیردرخت راس ۲ (شامل رئوس ۲، ۴ و ۵) را بگوید، که مسیر ۵ ۲ ۴ و به طول ۲ است.

در ثانیه‌ی سوم، کاراکتر اصلی ۱ باید بلندترین مسیر با شروع از راس ۷ در زیردرخت خود راس ۷ را بگوید. چون راس ۷ برگ است و زیردرخت راس ۷ فقط شامل خودش است، پس طول بلندترین مسیر در آن ۰ است.