• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

شازززیا دارند یک سری آزمون برای بچه‌ها آماده می‌کنند. از آنجایی که خیلی پای آن زحمت کشیده‌اند دوست دارند که کلی تبلیغش کنند تا همه‌ی بچه‌ها در آزمون‌ها شرکت کنند رو این حساب می‌خواهند تو شازززلند لوگوی آزمون‌هایشان را پخش کنند و برای این کار تصمیم گرفتند از کل ساختمان‌های خیابان اصلی بعنوان بخشی از لوگو استفاده کنند.

لوگو به شکل $n$ خط راه راه عمودی است که طول‌هایشان متفاوت است و از چپ به راست با $1$ تا $n$ شماره‌گذاری شده‌اند. لوگو با یک جایگشت به شکل $(s_1, s_2, .... , s_n)$ از اعداد $1$ تا $n$ نمایش داده می‌شود، به طوری که خط شماره $s_1$ کوتاه‌ترین خط باشد و بعد از آن بین سایر خط‌ها، خط شماره‌ی $s_2$ کوتاه‌ترین باشد و الی آخر تا آنکه خط شماره $s_n$ بلندترین باشد. طول واقعی خط‌ها اهمیت خاصی ندارد. (صرفا ترتیبشان از نظر اندازه مهم است)

در خیابان اصلی شازززلند $m$ تا ساختمان وجود دارد که طول‌هایشان متفاوت است. حالا شازززیا که این مسئله را به شکل یک سوال الگوریتمی می‌دیدند تصمیم گرفتند تعداد بازه‌هایی را پیدا کنند که لوگو با ساختمان‌های آن بازه مچ می‌شود.

اما از آن جایی که شازززیا مشغول آماده کردن سوالات هستند نمی‌توانند خودشان این سوال را حل کنند. پس به آن‌ها کمک کنید که تعداد زیردنباله‌های پیوسته از دنباله ساختمان‌ها را که با لوگو مچ می‌شوند را پیدا کنند. یک دنباله پیوسته از ساختمان‌ها با لوگو مچ می‌شود اگر ساختمان شماره $s_1$ بین دنباله کوتاه ترین باشد و بعد ساختمان شماره $s_2$ دومین کوتاه ترین باشد (یعنی بین همه ساختمان‌ها بجز ساختمان شماره $s_1$ کوتاه ترین باشد) و الی آخر تا ساختمان شماره $s_n$ که بلندترین باشد. برای مثال یک دنباله از ساختمان‌ها با ارتفاع‌های $5,10,4$ با لوگویی مچ می‌شود که به شکل جایگشت $(3,1,2)$ باشد؛ از آنجایی که ساختمان شماره $3$ با ارتفاع $4$ از همه کوتاه تر است و ساختمان شماره $1$ دومین کوتاه ترین است و ساختمان شماره $2$ بلندترین است.

ورودی

در سطر اول ورودی دو عدد $n$ نشان دهنده تعداد خط‌های لوگو و $m$ نشان دهنده تعداد ساختمان‌های خیابان اصلی شازززلند آمده است. $$ 2 \le n \le m \le 1000,000 $$ در سطر دوم ورودی جایگشت $s$ از اعداد $1$ تا $n$ که لوگو با آن نشان داده می‌شود، آمده است. اگر $ i \neq j $ آنگاه $ s_i \neq s_j $ است. $$ 1 \le s_i \le n $$ در سطر سوم ورودی $m$ عدد آمده است که $h_i$ ارتفاع ساختمان $i$‌ام در خیابان اصلی است. همه‌ی $h_i$ها متفاوتند. $$ 1 \le i \le m $$$$1 \le h_i \le 1000,000 $$

خروجی

در تنها سطر خروجی تعداد زیردنباله‌های پیوسته از دنباله ساختمان‌ها را که با لوگو مچ می‌شود را چاپ کنید.

زیرمسئله‌ها

زیرمسئله	نمره	محدودیت
۱	۲۰	$$ n \le 5000\ ,\ m \le 20,000$$
۲	۳۰	$$ n \le 50,000\ ,\ m \le 200,000$$
۳	۳۰	آرایه $h$ حداکثر $3000,000$ نا‌به‌جایی دارد
۴	۲۰	بدون محدودیت اضافی

مثال

ورودی نمونه ۱

5 10
2 1 5 3 4
5 6 3 8 12 7 1 10 11 9

خروجی نمونه ۱

2

توضیح نمونه:

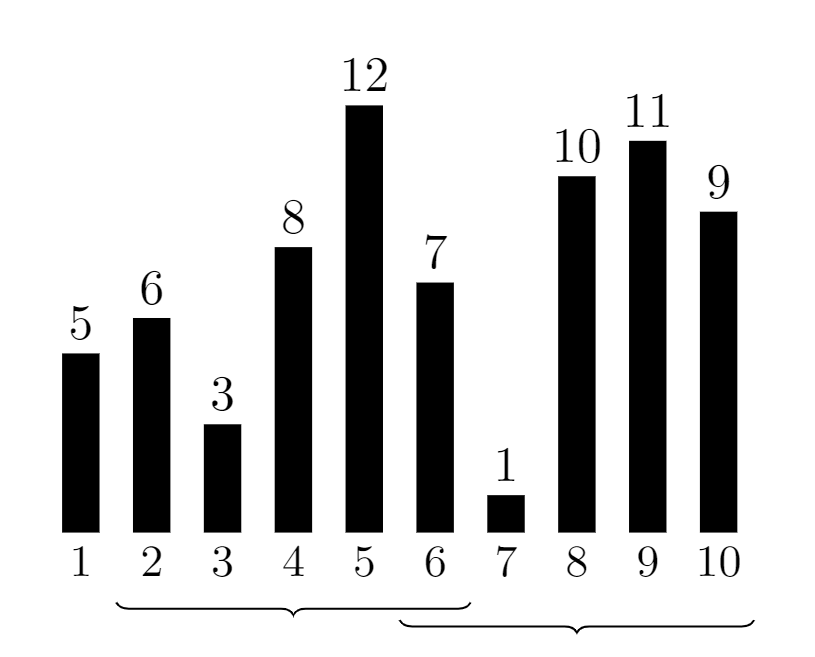هر دو دنباله $6, 3, 8, 12, 7$ و $7, 1, 10, 11, 9$ با لوگوی نشان داده شده با جایگشت $(2, 1, 5, 3, 4)$ مچ می‌شوند.