- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
مانی به تازگی استخدام شده که خانهای بسازد! اولین مشکل مانی برای شروع، صافی زمین زیر خانه بود. به طور دقیقتر زمین زیر خانه به شکل جدولی از راست نامتناهی بود که ارتفاع ستون $i$ام آن (از سمت چپ) $h_i$ است. مانند مثال زیر: (نقطهها در جدول نشانگر ادامهدار و نامتناهی بودن جدول از سمت راست است، برای مثال $h_3=5$ و $h_7=0$ است)

برای صافکاری سطح، مانی میتواند از ترکیب این دو عملیات استفاده کند:
- یک خانه خاک به یک ستون اضافه کند و $a$تا هزینه دهد.
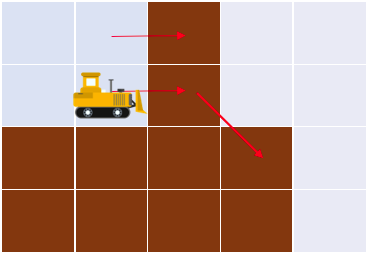
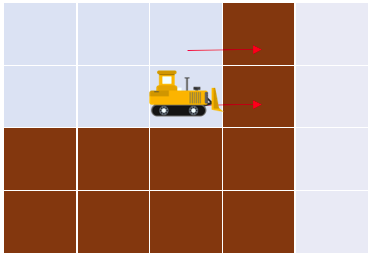
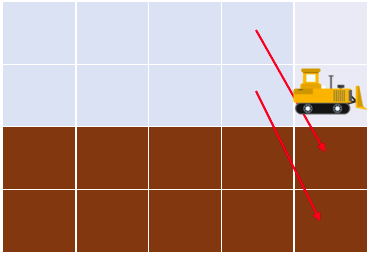
- با بولدوزر از بالای چپترین ستون زمین شروع کرده و به سمت راست برود. اگر ارتفاع ستون بعدی از ستونی که در آن است بیشتر بود، خاکهای آن ستون را به ستون بعدی هل بدهد و اگر ارتفاع ستون بعدی کمتر از ستون کنونی بود، متوقف شود. همچنین هزینهی کل این عملیات $b$ واحد است. (برای توضیحات بیشتر به مثال نمونه ۱ توجه کنید.)
توجه کنید هدف همارتفاع کردن ستونهایی است که حداقل یک واحد خاک دارند. به عبارت دیگر در آخر ارتفاع همهی ستونهایی که حداقل یک واحد خاک دارند باید برابر باشد. حال به مانی کمک کنید که با کمترین هزینه زمین را صاف کند.
ورودی
در خط اول ورودی به ترتیب $n$، $a$ و $b$ داده میشود. $$1 \le n \le 2000$$ $$1 \le a, b \le 10^9$$
در خط دوم ورودی $n$ عدد آمده که $i$امین آنها برابر با ارتفاع ستون $i$ام یا همان $h_i$ است. $$1 \le h_i \le 2000$$ توجه کنید برای $i > n$ مقدار $h_i$ برابر با صفر است.
خروجی
در تنها خط خروجی، کمینهی هزینه را چاپ کنید.
مثال
ورودی نمونه ۱
4 7 9
2 4 3 1
خروجی نمونه ۱
9
میتوان با یکبار انجام عملیات ۲ به جواب رسید. در این مثال $n=4$ است. توجه کنید خاکها میتوانند به خانههای بعد از $n$ ستون اول نیز برسند

ورودی نمونه ۲
6 1 3
3 2 5 1 4 4
خروجی نمونه ۲
5
مثال مربوط به شکل اول سوال است که میتوان به ترتیب زیر عملیاتها را انجام داد:
- یک خانه خاک به ستون دوم اضافه کنیم و ۱ واحد هزینه دهیم.
- یکبار عملیات نوع ۲ را انجام دهیم و ۳ واحد هزینه دهیم.
- یک خانه خاک به ستون هفتم اضافه کنیم و ۱ واحد هزینه دهیم.
در آخر جمع هزینههای این مثال برابر با ۵=۱+۳+۱ خواهد شد.
ورودی نمونه ۳
1 5 6
10
خروجی نمونه ۳
0
در این مثال تنها یک ستون وجود دارد و زمین از همان ابتدا صاف است.
ارسال پاسخ برای این سؤال