• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

علی در شهری نامتناهی زندگی می‌کند که خیابان‌های آن مانند شکل زیر است. شما می‌توانید خانه علی که در یکی از تقاطع‌های این شهر قرار دارد را در تصویر زیر ببیند.

علی در خانه مانده و حوصله‌اش خیلی سررفته و می‌خواهد در شهر گشتی بزند. گشت زدن علی \(n\) مرحله دارد. علی در هر مرحله یکی از ۶ جهت که با حروف \(\{ A, B, C, D, E, F \}\) در شکل نشان‌داده‌ایم را انتخاب می‌کند و از محل تقاطع فعلی در آن جهت حرکت می‌کند تا به تقاطع بعدی برسد.

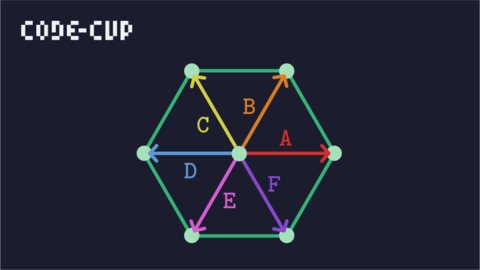
پس یک گشت علی را می‌توان به صورت یک رشته به طول \(n\) مثل:\[s_1, s_2, s_3, \dots, s_n\] نشان داد به طوری که برای هر \(i\) از ۱ تا \(n\): \[s_i \in \{A, B, C, D, E, F\}\]

علی می‌خواهد برای هر یک از \(t\) گشتی که انتخاب کرده است، فاصله‌ی نقطه‌ی پایانی این گشت را با خانه حساب کند.

منظور از فاصله دو تقاطع، یعنی طول کوتاه‌ترین گشتی که بتوان با کمک آن از یک تقاطع به تقاطع دیگر رفت. همچنین فاصله دو تقاطع یکسان را ۰ در نظر می‌گیریم.

ورودی

در سطر اول ورودی عدد صحیح و مثبت \(t\) آمده است. که نشان‌دهنده‌ی تعداد گشت‌هایی است که در این ورودی آمده است. \[1 \le t \le 1 \, 00 \, 000\] در \(t\) سطر بعدی، در هر سطر یک رشته که تنها شامل حروف \(\{ A, B, C, D, E, F \}\) است آمده که نشان‌دهنده یک گشت علی است.

تضمین می‌شود مجموع طول رشته‌ها در یک ورودی از ۱۰۰,۰۰۰ بیشتر نشود.

خروجی

خروجی شامل \(t\) سطر است که در هر سطر یک عدد صحیح و نامنفی، که نشان‌دهنده فاصله تقاطع نهایی علی بعد از انجام آن گشت تا تقاطعی که خانه علی در آن قرار دارد است.

مثال

ورودی نمونه

3
A
AB
ABC

خروجی نمونه

1
2
2

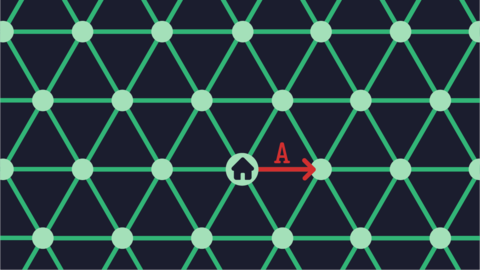
شکل حرکت علی در گشت اول.

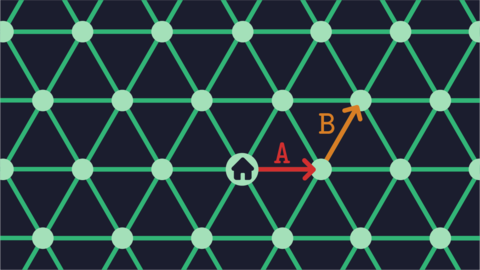
شکل حرکت علی در گشت دوم.

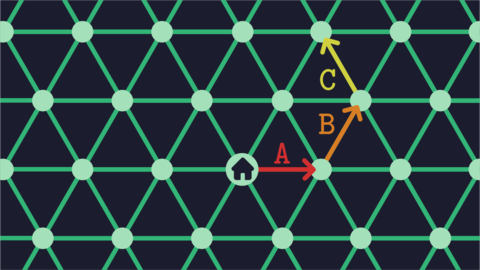
شکل حرکت علی در گشت سوم.