• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

امروز روز جهانیه ریاضیاته! و «نظریه گراف‌ها» یکی از مدل‌های باحال اونه...

%align_center_start%

دکتر مهدی بهزاد

%align_end%

فرض کنید \(G = (V, E)\) و \(G' = (V', E')\) دو گراف ساده بدون جهت باشند. منظور \(G \times G'\) یعنی گرافی که راس‌های آن \(V \times V'\) (ضرب دکارتی) باشد و یک یال بین دو راس \((v, v')\) و \((u, u')\) وجود دارد اگر و تنها اگر \(v = u\) و \(v'u'\) یالی در \(G'\) باشد یا \(v' = u'\) و \(vu\) یالی در \(G\) باشد.

به همین ترتیب می‌توان تعریف را تعمیم داد و \(k\) گراف را در هم ضرب کرد!

حال فرض کنید گراف \(G\) داده شده است و منظور از \(G^k\) گرافی است که از \(k\) بار ضرب شدن \(G\) در خودش بدست می‌آید.

می‌دانیم راس‌های \(G^k\) دنباله‌هایی به طول \(k\) از راس‌های \(G\) خواهند بود. دو راس \(v_1, v_2, \dots, v_k\) و \(u_1, u_2, \dots, u_k\) در این گراف را در نظر بگیرید. این دو راس به هم با یک یال متصل خواهند بود اگر و تنها اگر یک اندیس \(i\) وجود داشته باشد که \(v_i\) و \(u_i\) در گراف \(G\) با یک یال به هم متصل باشند و به ازای همه‌ی اندیس‌های \(j\) که \(i \neq j\) داشته باشیم \(v_j = u_j\).

به شما دو راس از \(G^k\) داده می‌شود و شما باید طول کوتاه ترین مسیر بین این دو راس را محاسبه کنید.

ورودی

در سطر اول ورودی دو عدد صحیح و مثبت \(n\) و \(m\) داده می‌شود که به ترتیب نشان‌دهنده‌ی تعداد راس‌ها و یال‌های \(G\) است. \[1 \leq n \leq 500\] \[0 \leq m \leq \frac{n(n - 1)}{2}\] در \(m\) سطر بعدی در هر سطر دو عدد صحیح و مثبت \(u\) و \(v\) آمده که نشان‌دهنده‌ی یال گراف \(G\) است. \[1 \leq u \neq v \leq n\] تضمین می‌شود هیچ یالی دوبار ظاهر نشود یعنی \(G\) گرافی ساده خواهد بود.

در سطر بعدی عدد صحیح و مثبت \(k\) آمده است. \[1 \leq k \leq 500 \ 000\] در سطر بعدی \(k\) عدد صحیح و مثبت \(v_1, v_2, \dots, v_k\) با فاصله آمده است و در سطر بعدی \(k\) عدد صحیح و مثبت \(u_1, u_2, \dots, u_k\) آمده است و به ترتیب نشان‌دهنده دو راس در \(G^k\) هستند. \[ 1 \le u_i, v_i \le n \]

خروجی

در تنها سطر خروجی پاسخ مسئله یعنی کوتاه ترین مسیر بین این دو راس را چاپ کنید. در صورتی که مسیری بین این دو راس وجود نداشته باشد عدد منفی یک را چاپ کنید.

مثال

ورودی نمونه ۱

3 2
1 2
2 3
3
1 2 3
1 3 1

خروجی نمونه ۱

3

گراف داده شده به صورت زیر است:

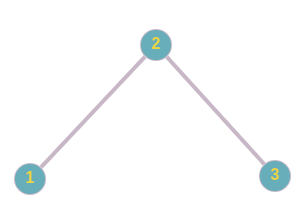
دنباله مسیر از \((1, 2, 3)\) به \((1, 3, 1)\) به صورت زیر خواهد بود.

\[(1, 2, 3) \to (1, 3, 3) \to (1, 3, 2) \to (1, 3, 1)\]

ورودی نمونه ۲

4 2
1 2
3 4
2
1 4
2 2

خروجی نمونه ۲

-1

گراف داده شده به صورت زیر است:

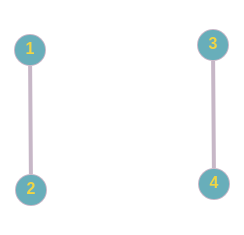
و هیچ مسیری از \((1, 4)\) به \((2, 2)\) وجود ندارد.