- محدودیت زمان: ۰.۵ ثانیه
- محدودیت حافظه: ۶۴ مگابایت
امروز روز جهانیه ریاضیاته! و «هندسه» یکی از مباحث قدیمی اونه...
%align_center_start%
دکتر سیاوش شهشهانی
%align_end%
امیرحسام دو تکه چوب با طول‌های $a$ و $b$ دارد. او می‌خواهد دقیقاً یکبار یکی از این دو تکه چوب را بردارد و به دو تکه چوب با طول‌های حقیقی و مثبت (نه لزوماً برابر) تقسیم کند.
منظور از تقسیم کردن یک چوب با طول $l$ یعنی آن را به دو چوب با طول‌های مثبت $y$ و $l - y$ تبدیل کنیم.
او می‌خواهد طوری این تقسیم را انجام دهد به طوری که بتوانیم با سه تکه چوب جدید، اضلاع مثلثی با مساحت ناصفر بسازیم. بررسی کنید آیا امیرحسام می‌تواند چنین کاری را انجام دهد یا نه.
با سه تکه چوب با طول‌های حقیقی و مثبت $x$، $y$ و $z$ می‌توان یک مثلث با مساحت ناصفر ساخت اگر و تنها اگر $$x + y > z, \quad x + z > y, \quad y + z > x$$
ورودی
در سطر اول ورودی دو عدد صحیح و مثبت $a$ و $b$ که با یک فاصله از هم آمده‌اند و نشان‌دهنده طول چوب‌ها است.
$$1 \le a, b \le 100$$
خروجی
در تنها سطر خروجی، در صورتی که انجام این کار شدنی است؛ کلمه YES و در غیر این صورت NO را چاپ کنید.
توجه کنید سیستم داوری به بزرگی و کوچکی حروف حساس است.
مثال‌ها
ورودی نمونه ۱
2 3
خروجی نمونه ۱
YES
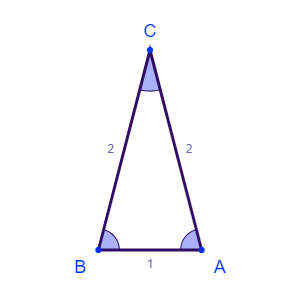
انجام این کار ممکن است، چوب دوم با طول ۳ را به دو قسمت با طول ۱ و ۲ تقسیم می‌کنیم. در این صورت طول این تکه چوب‌ها ۲، ۲، ۱ خواهد بود که می‌توان با آن‌ها مثلث ساخت.
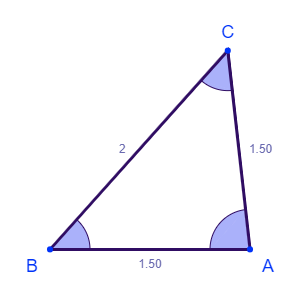
توجه کنید این روش تقسیم یکتا نیست برای مثال می‌توان چوب با طول ۳ را به دو قسمت با طول ۱.۵ و ۱.۵ تقسیم کنیم و با سه تکه چوب با طول‌های ۱.۵، ۱.۵ و ۲ می‌توان مثلث ساخت.
ورودی نمونه ۲
2 2
خروجی نمونه ۲
NO
هیچ روشی برای تقسیم کردن یک چوب و ساختن یک مثلث با مساحت ناصفر با اضلاع این سه چوب وجود ندارد.
ارسال پاسخ برای این سؤال