- محدودیت زمان: ۴ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
- منبع: سایت acm.sgu
تیم بسکتبال دانشکده مدتی است که از دوران اوج خود خارج فاضله گرفته و به افول دچار شده است. کیانوش علت این امر را در دفاع خطی ۴تایی یا همان "سطحسطحسحطسطح" می‌داند. برای حل این مشکل او قصد دارد سیستم دفاع خطی ۶تایی یا "سطحسطحسحطسطحسطحسحط" را در تیم پیاده کند. در این سیستم بازیکنان مطابق شکل زیر در ۳۱ شش‌ضلعی مجاور چیده می‌شوند.
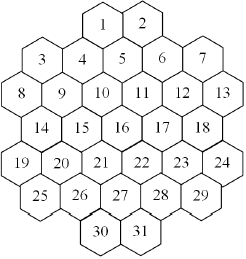
می‌دانیم شماره لباس هریک از اعضای تیم یکی از اعداد ۱ تا $k$ است و اگر دو نفر شماره لباس یکسان داشته باشند، به دلایل شخصی(!) دوست ندارند در یک سطر ( در هر یک از ۳ جهت ممکن) قرار بگیرند. هم‌چنین در هر یک از شش‌ضلعی‌های کوچک‌تر شامل ۷خانه که مرکز آن‌ها با خانه‌های سیاه مشخص شده است نیز نباید ۲ بازیکن با شماره لباس یکسان قرار بگیرند. (می‌توانید چند نمونه از سطرها و شش‌ضلعی‌های ۷ خانه‌ای را در دو شکل زیر ببینید.)
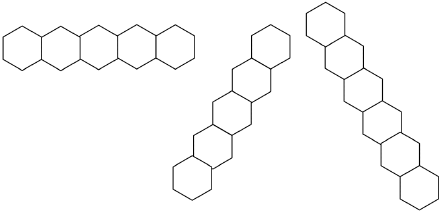در شکل بالا منظور از سه جهت ممکن از سطرها مشخص شده.
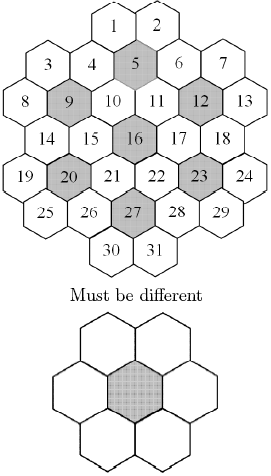
در شکل بالا هردوتا از ۷ عدد موجود در شش‌ضلعی‌های دور یک خانه سیاه و خودش باید متفاوت باشند.
هم‌چنین شماره لباس برخی از بازیکنان نیز از قبل مشخض شده است و غیرقابل تغییر است. حال کیانوش باید شماره لباس سایر دانشجویان را طوری تعیین کند که شرایط بالا برقرار باشد. هم‌اکنون کیانوش درگیر مذاکرات پیچیده با دانشجویان حول مبحث "نقض قوانین حق تکثیر و استفاده از عکس شخصی وی به عنوان عکس پروفایل" است، پس از شما خواسته که یک چینش مناسب برای تیم ارائه کنید.
ورودی
در خط اول ورودی عدد طبیعی $k$ آمده است: $$1 \le k \le 31$$ در خط بعدی ۳۱ عدد آمده است که عدد $i$ ام نشان‌دهنده این است که لباس دانشجوی خانه $i$ ام چه شماره‌ای دارد. اگر این عدد ۰ باشد، یعنی کیانوش می‌تواند لباس با هر شماره‌ای که میخواهد را به او بدهد.
تضمین می‌شود که ورودی طوری انتخاب می‌شود که حداقل یک شماره‌دهی مناسب وجود داشته باشد.
خروجی
در تنها خط خروجی یک شماره‌دهی مناسب برای لباس افراد ارائه دهید. در صورت وجود چند خروجی متفاوت، یکی را به دل‌خواه خروجی دهید.
مثال
ورودی نمونه
8
1 0 0 3 0 0 0 0 4 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0
خروجی نمونه
1 2 1 3 4 5 2 2 4 6 7 1 3 7 5 1 8 6 2 1 3 4 5 7 8 6 7 2 3 5 8
خروجی مطابق مثال بالا را می‌توانید در شکل زیر مشاهده کنید:
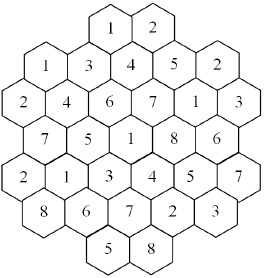
ارسال پاسخ برای این سؤال