• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

الکس تاو (Alex Tew) یک ایده بسیار جالب دارد و می‌توانید ماجرای اصلی آن را اینجا بخوانید. اما داستان تحریف شده آن را در ادامه آورده‌ایم.

او در صفحه اول یک وب‌سایت یک بنر $n \times m$ پیکسل قرار داده است. او قیمت هر پیکسل را یک دلار قرار داده است.

اما او یک قانون دارد، آن هم این که هر کس می‌تواند یک بلوک $a \times b$ از این صفحه را بخرد که قبلا هیچ پیکسلی از آن به فروش نرسیده باشد.

حال امین می‌خواهد تعدادی از پیکسل‌ها را بخرد به طوری که:

• هیچ کس نتواند هیچ پیکسل دیگری بخرد.
• کمترین هزینه را صرف این کار کند.

ورودی

در سطر اول ورودی، عدد صحیح $T$ آمده، که تعداد تست‌کیس‌ها را نشان‌می‌دهد. $$1 \leq T \leq 100$$

در $T$ سطر بعدی، در هر سطر چهار عدد صحیح $n$، $m$، $a$ و $b$ آمده که به ترتیب تعداد سطر و ستون‌های سایت و ابعاد بلوک‌های مجاز برای خریدن است.

$$1 \leq a \leq n \leq 1000, \quad \quad 1 \leq b \leq m \leq 1000$$

خروجی

خروجی $T$ سطر دارد که کمترین تعداد بلوک لازم برای رسیدن به هدف امین را نشان می‌دهد.

مثال

ورودی نمونه ۱

3
5 7 1 1
10 10 2 3
5 7 2 1

خروجی نمونه ۱

35
6
14

تست اول.

اگر صفحه اصلی $5\times7$ باشد و امکان خرید بلوک‌های $1\times1$ باشد، باید همه $35$ خانه را بخرد تا کسی نتواند هیچ بلوک دیگری را بخرد.

تست دوم.

اگر صفحه اصلی $10\times10$ باشد و امکان خرید بلوک‌های $2\times 3$ باشد‌، می‌تواند با خریدن $6$ بلوک مانند تصویر پایین‌، کاری کند که هیچ‌کس نتواند بلوک دیگری بخرد. همچنین می‌توان نشان‌داد حداقل $6$ بلوک لازم است.

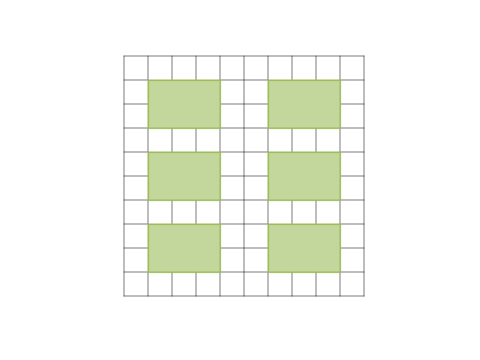
تست سوم.

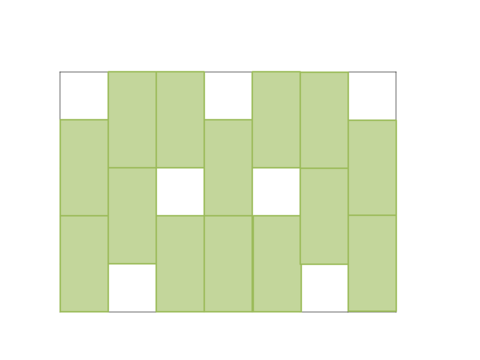
اگر صفحه اصلی $5\times7$ باشد و امکان خرید بلوک‌های $2\times 1$ باشد‌، می‌تواند با خریدن $14$ بلوک مانند تصویر پایین‌، کاری کند که هیچ‌کس نتواند بلوک دیگری بخرد. همچنین می‌توان نشان‌داد حداقل $14$ بلوک لازم است.