• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

در گذشته‌ای نه چندان دور $n$ کشور داشتیم که یکی از آن‌ها آلمان نازی بود و به رهبری هیتلر به دنبال فتح جهان بودند. برای راحتی، کشورها و روابط بین آن‌ها را به شکل گرافی $n$ راسی و $m$ یالی نشان می‌دهیم که راس‌ها نشان دهنده‌ی کشور‌ها و یال‌ها نشان دهنده‌ی همسایگی دو طرفه بین کشورها است.

در ابتدا کشور $i$ام قدرت $a_i$ را دارد و یکی از آن‌ها آلمان نازی است. هیتلر در جهت کشورگشایی هر بار می‌تواند یک کشور جدید که حداقل یکی از همسایه‌هایش فتح شده را انتخاب کند، و اگر قدرت آلمان نازی بیشتر اکید از آن بود، آن کشور را فتح کند. پس از فتح یک کشور، به اندازه‌ی قدرت آن کشور، به قدرت آلمان نازی اضافه می‌شود.

سوالی که آن زمان فکر سیاست مداران را به خود درگیر کرده بود، این بود که آیا هیتلر می‌تواند موفق شود همه‌ی کشورها را فتح کند یا خیر؟ و اگر نمی‌تواند، حداقل چه مقدار باید قدرت آلمان نازی افزایش یابد تا بتواند به این هدف برسد؟ اما از آن‌جایی که هیتلر مخفی است و مکان اولیه آلمان نازی را نمی‌دانیم، شما باید به ازای هر کشور، این مقدار را محاسبه کنید!

ورودی

در سطر اول ورودی، دو عدد $n$ و $m$ به ترتیب نشان‌دهنده‌ی تعداد کشورها و تعداد روابط همسایگی بین کشورها می‌آیند.

$$ 1 \le n \le 1933, \quad\quad n-1 \le m \le 1945 $$

در سطر دوم ورودی، اعداد $a_1, a_2, \dots, a_n ,$ که قدرت کشورها را نشان می‌دهند، می‌آیند.

$$ 1 \le a_i \le 10^9 $$

در هر کدام از $m$ سطر بعدی، دو عدد $v$ و $u$ می‌آیند که نشان دهنده‌ی یالی بین راس $v$ام و راس $u$ام است.

$$ 1 \le v, u \le n, \quad\quad v \neq u $$

تضمین می‌شود گراف داده شده همبند باشد.

خروجی

در تنها سطر خروجی، باید $n$ عدد با فاصله از هم چاپ کنید که عدد $i$ام حداقل مقداری است که باید به کشور $i$ام اضافه کنیم تا در صورتی که آلمان نازی این کشور باشد، بتواند همه‌ی کشورها را فتح کند. (ممکن است این مقدار $0$ باشد.)

مثال‌ها

ورودی نمونه ۱

3 2
1 2 3
1 2
2 3

خروجی نمونه ۱

2 1 0

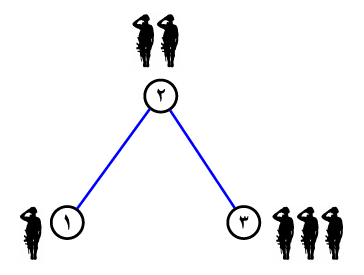
اگر مکان اولیه آلمان نازی:

• کشور ۱ باشد و با قدرت $3$ شروع به کار کند، ابتدا می تواند کشور ۲ را فتح کند تا قدرتش $5$ شود. سپس می‌تواند کشور ۳ را فتح کند و به هدفش برسد. بنابراین باید حداقل $2$ واحد به قدرتش اضافه کند.

• کشور ۲ باشد و با قدرت $3$ شروع به کار کند، ابتدا می تواند کشور ۱ را فتح کند تا قدرتش $4$ شود. سپس می‌تواند کشور ۳ را فتح کند و به هدفش برسد. بنابراین باید حداقل $1$ واحد به قدرتش اضافه کند.

• کشور ۳ باشد و با قدرت $3$ شروع به کار کند، ابتدا می تواند کشور ۲ را فتح کند تا قدرتش $5$ شود. سپس می‌تواند کشور ۱ را فتح کند و به هدفش برسد.

می‌توان نشان داد اگر با قدرتی کمتر از این مقدار شروع کند، نمی‌تواند به هدفش برسد.

ورودی نمونه ۲

7 10
16 1 32 256 4 128 64
2 6
6 7
1 2
3 7
5 4
7 5
6 2
4 2
4 6
6 3

خروجی نمونه ۲

112 112 33 0 61 12 29

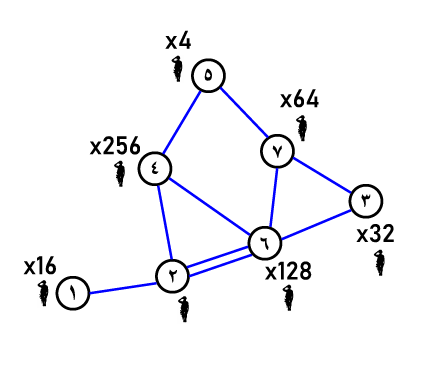
اگر مکان اولیه آلمان نازی:

• کشور ۱ باشد و با قدرت $128$ شروع به کار کند، ابتدا می‌تواند کشور ۲ را فتح کند تا قدرتش $129$ شود. سپس می‌تواند کشور ۶ را فتح کند تا قدرتش $257$ شود. اکنون می‌تواند به ترتیب کشورهای ۳، ۴، ۵ و ۷ را فتح کند و به هدفش برسد. بنابراین باید حداقل $112$ واحد به قدرتش اضافه کند.

• کشور ۲ باشد و با قدرت $128$ شروع به کار کند، ابتدا می‌تواند کشور ۱ را فتح کند تا قدرتش $129$ شود. سپس همان روال کشور ۱ را می‌توان ادامه داد.

• کشور ۳ باشد و با قدرت $65$ شروع به کار کند، ابتدا می‌تواند کشور ۷ را فتح کند تا قدرتش $129$ شود. اکنون می‌تواند به ترتیب کشور ۶، ۵، ۴، ۲ و ۱ را فتح کند و به هدفش برسد.

• کشور ۴ باشد و با قدرت $256$ شروع به کار کند، می‌تواند به ترتیب کشورهای ۲، ۱، ۵، ۶، ۳ و ۷ را فتح کند و به هدفش برسد.

• کشور ۵ باشد و با قدرت $65$ شروع به کار کند، ابتدا می‌تواند کشور ۷ را فتح کند تا قدرتش $129$ شود. سپس می‌تواند کشور ۶ را فتح کند تا قدرتش $257$ شود. سپس می‌تواند به ترتیب کشورهای ۴، ۳، ۲ و ۱ را فتح کند و به هدفش برسد.

• کشور ۶ باشد و با قدرت $140$ شروع به کار کند، ابتدا می‌تواند به ترتیب کشورهای ۲، ۳، ۷، ۵ و ۱ را فتح کند تا قدرتش $257$ شود. در نهایت می‌تواند کشورهای ۴ را فتح کند و به هدفش برسد.

• کشور ۷ باشد و با قدرت $93$ شروع به کار کند، ابتدا می‌تواند کشور ۵ را فتح کند تا قدرتش $97$ شود. سپس می‌تواند کشور ۳ را فتح کند تا قدرتش $129$ شود. سپس می‌تواند کشور ۶ را فتح کند تا قدرتش $257$ شود. در نهایت می‌تواند به ترتیب کشورهای ۴، ۲ و ۱ و به هدفش برسد.

می‌توان نشان داد اگر با قدرتی کمتر از این مقدار شروع کند، نمی‌تواند به هدفش برسد.