• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

امین در یک درخت زندگی می‌کند. این درخت $n$ راس دارد. راس‌های این درخت با $n - 1$ یال به هم متصل شده‌اند. طول یال $i$ برابر $\ell_i$ متر است.

امین در راس شماره $1$ این درخت زندگی می‌‌کند. او می‌خواهد یک روز برای خرید در این درخت گشتی بزند و سپس به راس $1$ بازگردد. او نمی‌خواهد از یک جاده بیش از دو بار عبور کند.

او می‌داند که قصد رفتن به راس‌های $v_1, v_2, \dots, v_k,$ را دارد و در هرکدام از آن‌ها باید یک خرید $w_1, w_2, \dots, w_k,$ کیلوگرمی انجام دهد.

همچنین به‌ازای هر متر که یک خرید $m$ کیلویی را حمل می‌کند. به اندازه‌ی $m$ خسته می‌شود.

حال از شما می‌خواهیم این گشت امین را طوری برنامه‌ریزی کنید که همه‌ی خریدهایش را انجام دهد و به راس شماره‌ی ۱ برساند و کمینه خستگی را تحمل کند.

ورودی

در سطر اول ورودی عدد صحیح و مثبت $n$ آمده که تعداد راس‌های درخت را نشان می‌دهد. $$2 \leq n \leq 300 , 000$$ در $n - 1$ سطر بعدی در هر سطر، سه عدد $u_i, v_i, l_i$ که با یک فاصله از هم جدا شده‌اند می‌آید و به‌ترتیب نشان‌دهنده‌ی وجود یال بین راس‌های $u_i$ و $v_i$ به طول $\ell_i$ متر است.

$$1 \leq u_i \neq v_i \leq n, \quad \quad 1 \leq \ell_i \leq 1000$$

تضمین می‌شود که ورودی بالا برای یک درخت باشد.

در سطر بعدی عدد $k$ آمده که تعداد راس‌هایی که باید امین در آن‌ها خرید کند را نشان می‌دهد. $$1 \leq k \leq 300,000$$ در $k$ سطر بعدی، در هر سطر دو عدد $v_j$ و $w_j$ آمده که نشان می‌دهد خریدی در راس $v_j$ دارد که وزن آن برابر $w_j$ است.

$$2 \leq v_j \leq n, \quad \quad 1 \leq w_j \leq 1000$$

ممکن است راس‌هایی که در آن خرید داریم یکسان باشد ولی باید هر دو خرید را انجام دهیم.

خروجی

در تنها سطر خروجی، کمینه خستگی ممکن برای این گشت را محاسبه کنید.

مثال‌ها

ورودی نمونه ۱

5
1 2 1
1 3 2
2 4 1
2 5 2
3
4 10
2 3
3 4

خروجی نمونه ۱

47

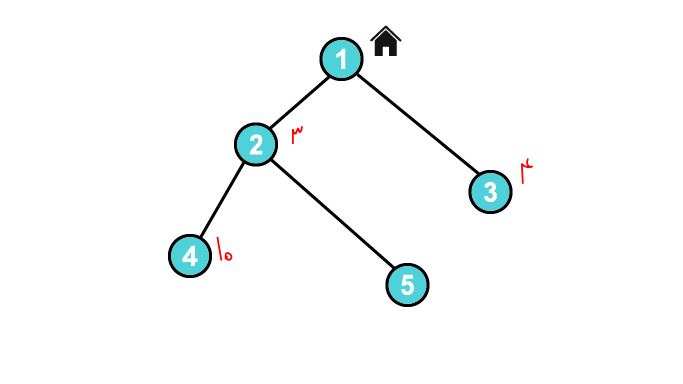
دنباله‌ی سفر خود را به این صورت انتخاب می‌کنیم: $$1 \to 3 \to 1 \to 2 \to 4 \to 2 \to 1$$

به این ترتیب «۶ متر خرید ۴ کیلوگرمی»، «۱ متر خرید ۳ کیلوگرمی» و «۲ متر خرید ۱۰ کیلوگرمی» حمل کردیم. بنابراین خستگی این گشت برابر است با:

$$6 \times 4 + 1 \times 3 + 2 \times 10 = 24 + 3 + 20 = 47$$

ورودی نمونه ۲

5
1 2 1
2 3 3
3 4 2
4 5 1
1
3 5

خروجی نمونه ۲

20

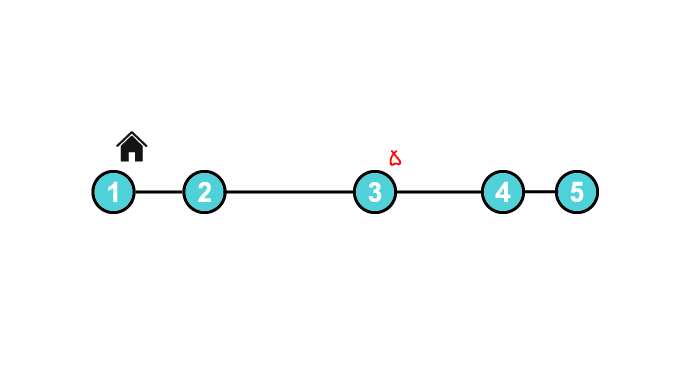
دنباله‌ی سفر خود را به این صورت انتخاب می‌کنیم: $$1 \to 2 \to 3 \to 2 \to 1$$

به این ترتیب «۴ متر خرید ۵ کیلوگرمی» حمل کردیم. بنابراین خستگی این گشت برابر است با:

$$4 \times 5 = 20$$