• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

درختی با $n$ راس داریم که هر راس آن ممکن است قرمز یا مشکی باشد (حداقل یک راس به رنگ قرمز موجود است). همینطور روی هر راس عددی نوشته شده است که می‌تواند مثبت، منفی یا صفر باشد.

زیردرختی از این درخت را در نظر بگیرید که شامل تمامی راس‌های قرمز بشود و مجموع اعداد راس‌هایش بیشینه باشد. از شما خواسته شده است که مجموع اعداد راس‌های این زیردرخت را چاپ کنید. منظور از زیردرخت مجموعه‌ای از راس‌ها است، که بدون استفاده از دیگر راس‌ها به همدیگر مسیر داشته باشند.

ورودی

در خط اول ورودی عدد $n$ آمده است که نمایانگر تعداد راس‌های درخت است.

در خط دوم رشته‌ای به طول $n$ آمده که هر کدام از حرف‌هایش می‌تواند R یا B باشد. حرف $i$-ام این رشته نشان‌دهنده‌ی رنگ راس $i$-ام است (R به معنای قرمز و B به معنای مشکی)

در خط بعدی $n$ عدد آمده است که عدد $i$-ام نمایانگر عدد راس $i$ است و آن را با $a_i$ نمایش می‌دهیم.

در نهایت در $n-1$ خط آخر، در هر خط دو عدد $u$ و $v$ آمده است که نشان‌دهنده‌ی وجود یال میان رئوس $u$ و $v$ است.

$$1 \le n \le 10^6$$ $$-10^9 \le a_i \le 10^9$$ $$1 \le u, v \le n$$

خروجی

در تنها خط خروجی باید پاسخ خواسته شده را چاپ کنید.

مثال

ورودی نمونه ۱

3
RBB
3 5 -2
1 2
1 3

خروجی نمونه ۱

8

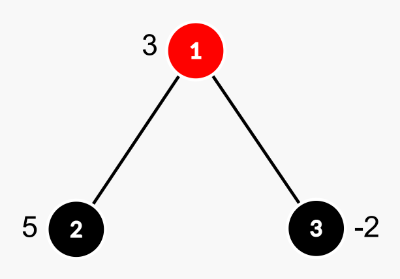
درخت این نمونه در شکل زیر نمایش داده شده است. بهترین حالت این است که زیردرختمان شامل راس‌های ۱ و ۲ باشد که مجموع آن‌ها ۸ است.

ورودی نمونه ۲

5
BBRRB
-3 2 4 2 1
1 2
1 3
3 4
3 5

خروجی نمونه ۲

7

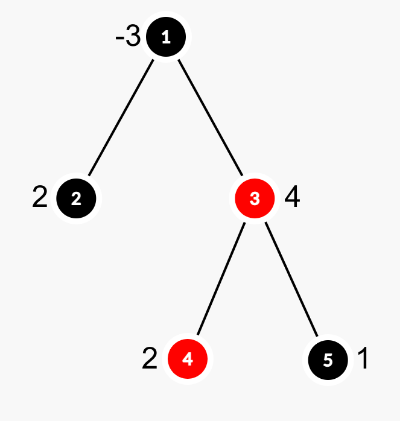
این درخت نیز در تصویر زیر پیداست، بهترین حالت این است که زیردرخت ما شامل رئوس ۳، ۴ و ۵ باشد. توجه کنید ممکن نیست راس ۲ به این رئوس اضافه شود، زیرا در آن صورت شرط زیردرخت بودن نقض می‌شود.

ورودی نمونه ۳

10
RBBBBBBBBB
2 1 -1 4 -2 3 2 -2 -1 3
1 2
1 3
1 4
2 5
2 6
3 7
3 8
4 9
8 10

خروجی نمونه ۳

12

ورودی نمونه ۴

13
BBRRBBRBRRBBB
8 -11 -2 3 12 7 -3 -16 7 2 4 5 4
1 2
1 3
1 4
2 5
3 6
3 7
4 8
4 9
4 10
7 11
7 12
9 13

خروجی نمونه ۴

36