• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

میدان اصلی شهر کدکاپ بسیار بزرگ است. دور این میدان $n$ چراغ روشنایی قرار دارد. این چراغ‌ها را با اعداد ۱ تا $n$ به ترتیب ساعت‌گرد شماره‌گذاری کرده‌اند.

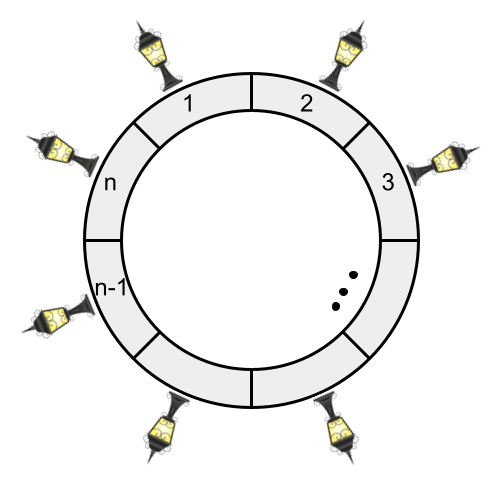
می‌دانیم اگر یک چراغ روشن شود، محوطه زیر آن و دو چراغ مجاورش روشن می‌شود. به صورت رسمی‌تر اگر چراغ شماره‌ی $i$ را روشن کنیم، ($1 \leq i \leq n$) محوطه‌ی زیر چراغ $i$، $i - 1$ و $i + 1$ روشن می‌شود. (اگر $i + 1$ از $n$ بیشتر شد به‌جای آن ۱ و اگر $i - 1$ از ۱ کمتر شد به‌جای آن $n$ را در نظر بگیرید.)

می‌دانیم هزینه‌ی روشن کردن شماره‌ی $i$ برابر $c_i$ است. می‌خواهیم با کمترین هزینه ممکن، تعدادی از چراغ‌ها را روشن کنیم به طوری که محوطه‌ی زیر همه‌ی چراغ‌ها روشن باشد.

ورودی

در سطر اول عدد $t$ آمده که تعداد تست‌ها را نشان می‌دهد. $$1 \leq t \leq 200 , 000$$

در هر خط یک عدد $n$ و سپس در خط بعد $n$ عدد نشان‌دهنده‌ی میزان هزینه برای روشن کردن هر چراغ را می‌گوییم.

$$1 \leq n \leq 200 , 000$$ $$1 \leq c_i \leq 1\ 000 , 000$$

تضمین می‌شود $\sum n$ برای همه‌ی تست‌ها حداکثر $200 , 000$ باشد.

خروجی

عدد نهایی نشان دهنده‌ی کمترین هزینه‌ای که تمام خیابان‌ها روشن شود را چاپ کنید.

مثال‌ها

ورودی نمونه ۱

5
5
1 1 1 2 2
3
3 4 7
5
7 5 4 1 1
1
100
7
4 4 4 4 4 4 4

خروجی نمونه ۱

2
3
5
100
12