• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

در کشور کدکاپ قدیم $n$ شهر با شماره‌های ۱ تا $n$ وجود داشته است. این کشور $n - 1$ جاده دو طرفه داشت و هر جاده دقیقاً دو شهر را به هم متصل می‌کرد. می‌دانیم در کدکاپ قدیم از هر شهری به هر شهر دیگر یک مسیر وجود داشته است (در واقع نقشه‌ی کشور کدکاپ به صورت یک درخت بوده است).

منظور از یک مسیر، دنباله‌ای از شهرهای مختلف مثل $v_1, v_2, \dots, v_k,$ است؛ به‌طوری که هر دو شهر متوالی با یک جاده به هم متصل شده باشد. طول این مسیر را $k$ می‌نامیم. منظور از بلندترین مسیر کشور، مسیری است که بین همه‌ی مسیرهای ممکن، بلندترین طول دارد.

اما اکنون نقشه‌ی کشور کدکاپ را از دست دادیم و برای هر شهر، تعداد جاده‌هایی که از آن خارج شده را می‌دانیم. می‌خواهیم با توجه به این عددها در بین تمام نقشه‌های ممکن برای کدکاپ قدیم، نقشه‌ای را در نظر بگیریم که طول بلندترین مسیر آن بیشینه است. از شما می‌خواهیم این طول را حساب کنید.

ورودی

در اولین خط ورودی عدد $n$ که نشان دهنده تعداد شهرهای کدکاپ قدیم داده می‌شود.

$$2 \leq n \leq 1 , 000 , 000$$

سپس در خط بعد $n$ عدد $d_i$ با فاصله از هم داده می شوند که عدد $i$ام یعنی $d_i$ نشان دهنده تعداد جاده‌های خارج شده از شهر $i$ است.

$$1 \leq d_i \leq n - 1$$

تضمین می‌شود از روی دنباله‌ی داده شده، حداقل یک نقشه برای کدکاپ قدیم می‌توان ساخت.

خروجی

شما باید در یک خط، طول بلندترین مسیر در نقشه‌ی کدکاپ قدیم را چاپ کنید.

مثال‌ها

ورودی نمونه ۱

4
1 2 2 1

خروجی نمونه ۱

4

توضیح نمونه ۱

---

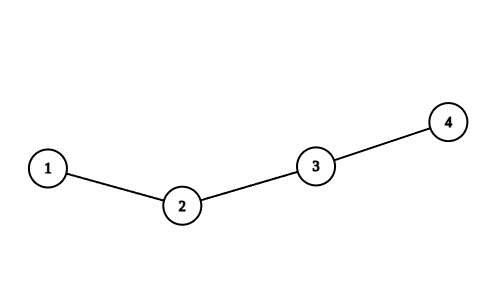
نقشه‌ی کدکاپ قدیم می‌تواند به صورت زیر باشد، تا تعداد جاده‌های خارج شده از هر شهر دقیقاً برابر اعداد ورودی باشد. بلند‌ترین مسیر آن $\langle 1, 2, 3, 4 \rangle$ است که طول آن ۴ است و این حداکثر مقدار ممکن است.

---

ورودی نمونه ۲

6
2 2 1 3 1 1

خروجی نمونه ۲

5

توضیح نمونه ۲

---

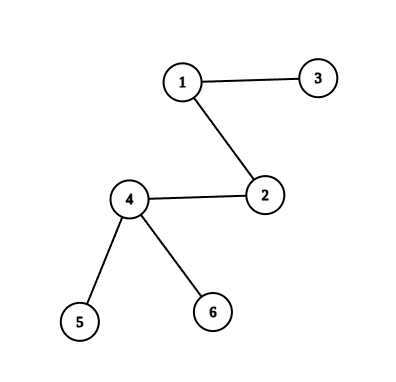
یکی از بلند‌ترین مسیرهای آن $\langle 3, 1, 2, 4, 5 \rangle$ است که طول آن ۵ است. و بین تمام حالت‌های قابل قبول دیگر برای نقشه‌ی کدکاپ قدیم، این مثال بیشترین طول را برای بلندترین مسیر دارد.

---