• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

شهر کدکاپ به صورت یک صفحه‌ی مختصات دو بعدی است. در این شهر آدم‌ها همیشه در نقطه‌هایی مثل $(x,y)$ قرار دارند که $x$ و $y$ دو عدد صحیح هستند. منظور از فاصله‌ی دو نقطه‌ی $(x, y)$ و $(a,b)$ عدد $|a - x| + |b - y|$ است.

یک پلیس در نقطه‌ی $(0, 0)$ قرار دارد. یک دزد از بانکی که در نقطه‌ی $(d, 0)$ قرار دارد دزدی می‌کند. آژیر خطر به صدا در می‌آید و بازی دزد و پلیس شروع می‌شود.

دزد در هر ثانیه یا در نقطه‌ی قبلی می‌ماند یا به یکی از نقطه‌های بالا، پایین، چپ یا راست می‌رود. یعنی اگر در نقطه‌ی $(x, y)$ باشد در ثانیه‌ی بعدی در یکی از نقطه‌های $(x, y)$، $(x + 1, y)$، $(x - 1, y)$، $(x, y + 1)$ یا $(x, y - 1)$‌ قرار دارد. در واقع دزد در یک ثانیه می‌تواند به نقطه‌ای که فاصله‌ی آن حداکثر ۱ است برود.

پلیس در هر ثانیه می‌تواند به نقطه‌ای که فاصله‌ی آن حداکثر ۲ است برود. می‌دانیم پلیس همیشه موقعیت دزد را می‌داند. او همیشه بر اساس موقعیت دزد نقطه‌ای که یک ثانیه بعد در آن است را مشخص می‌کند. اگر اکنون پلیس در نقطه‌ی $(x, y)$ و دزد نقطه‌ی $(a, b)$ باشد:

• اگر $|x - a| \gt |y - b|$ باشد پلیس به یکی از نقطه‌های $(x + 2, y)$، $(x + 1, y )$، $(x - 1, y)$ یا $(x - 2, y)$ می‌رود که به دزد نزدیک‌تر است.
• اگر $|x - a| \lt |y - b|$ باشد پلیس به یکی از نقطه‌های $(x, y+2)$، $(x,y+1)$، $(x,y-1)$ یا $(x,y-2)$ می‌رود که به دزد نزدیک‌تر است.
• اگر $|x - a| = |y - b|$ باشد پلیس به یکی از نقطه‌های $(x + 1,y+1)$، $(x-1,y+1)$، $(x+1,y-1)$ یا $(x-1,y-1)$ می‌رود.

برای راحتی کار فرض کنید آن‌ها یکی در میان حرکتشان را انجام می‌دهند یعنی ابتدا پلیس، سپس دزد، مجدداً پلیس، سپس دزد و... . با توجه به قوانین حرکت آن‌ها می‌توان فهمید بالاخره پلیس به نقطه‌ای که دزد در آن قرار دارد می‌رسد و دزد دستگیر می‌شود.

حال شهردار کدکاپ می‌خواهد بداند با توجه به حالت‌های مختلفی که حرکت دزد دارد، چند نقطه در صفحه وجود دارد که ممکن است در آن نقطه دزد توسط پلیس دستگیر شود.

برای بهتر متوجه شدن خواسته‌ی سوال به توضیح نمونه‌ها توجه کنید.

ورودی

در سطر اول ورودی، عدد صحیح و مثبت $t$ آمده که تعداد سناریوها را نشان می‌دهد. $$1 \leq t \leq 100 , 000$$

در $t$ سطر بعدی در هر سطر عدد صحیح و مثبت $d$ که موقعیت دزد را نشان می‌دهد داده می‌شود.

$$1 \leq d \leq 10^9$$

خروجی

خروجی $t$ سطر دارد که برای هر سناریو، تعداد نقاطی که دزد ممکن است در آن دستگیر شود را چاپ کنید.

مثال‌ها

ورودی نمونه ۱

3
2
5
9

خروجی نمونه ۱

1
21
85

توضیح نمونه ۱

در این سناریو پلیس در نقطه‌ی $(0,0)$ و دزد در نقطه‌ی $(2,0)$ قرار دارد.

در ثانیه‌ی اول پلیس $|2 - 0| \gt |0 - 0|$ را محاسبه کرده و تصمیم می‌گیرد به یکی از نقاط $(2,0)$، $(1,0)$، $(-1,0)$ یا $(-2,0)$ برود که به دزد نزدیک‌تر است. از آن‌جایی که دزد در نقطه‌ی $(2,0)$ قرار دارد قبل از اینکه حرکت کند دستگیر می‌شود.

چون فقط یک نقطه وجود دارد که دزد ممکن است در آن دستگیر شود، پاسخ برابر ۱ است.

توضیح نمونه ۲

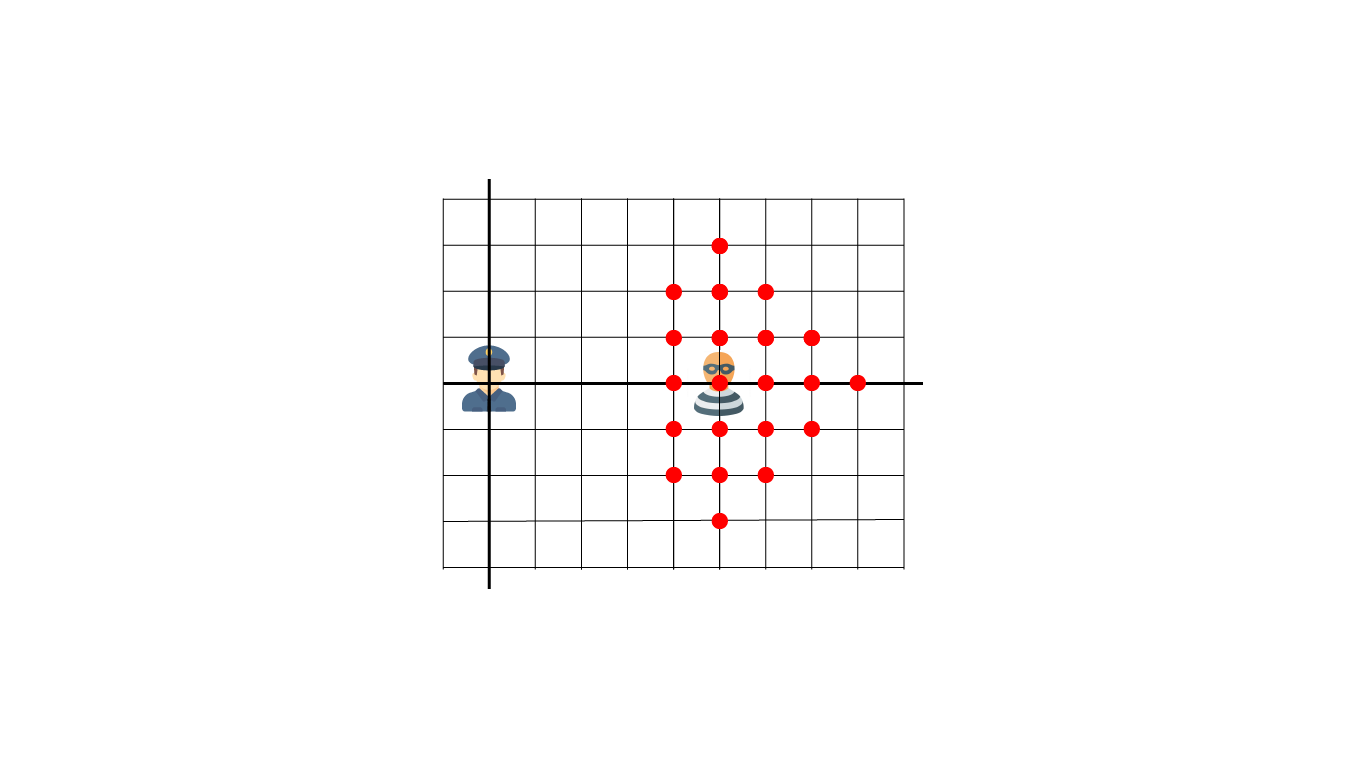
در ثانیه‌ی اول پلیس $|5 - 0| \gt |0 - 0|$ را محاسبه کرده و تصمیم می‌گیرد به یکی از نقاط $(2,0)$، $(1,0)$، $(-1,0)$ یا $(-2,0)$ برود که به دزد نزدیک‌تر است. از آن‌جایی که نقطه‌ی $(2,0)$ به دزد نزدیک‌تر است آن را انتخاب می‌کند. سپس نوبت دزد است که در ثانیه‌ی اول حرکت کند. فرض کنید او تصمیم می‌گیرد به نقطه‌ی بالایی یعنی $(5,1)$ برود.

در ثانیه‌ی دوم پلیس $|5-2| \gt |0 - 1|$ را محاسبه کرده و تصمیم می‌گیرد به یکی از نقاط $(4,0)$، $(3,0)$، $(1,0)$ یا $(0,0)$ برود که به دزد نزیک‌تر است. از آن‌جایی که نقطه‌ی $(4,0)$ به دزد نزدیک‌تر است آن را انتخاب می‌کند. سپس نوبت دزد است که در ثانیه‌ی دوم حرکت کند. فرض کنید تصمیم می‌گیرد سر جای خودش یعنی $(5,1)$ بماند.

در ثانیه‌ی سوم پلیس $|4-5| = |1-0|$ را محاسبه می‌کند و تصمیم می‌گیرد به یکی از نقاط $(5,1)$، $(5,-1)$، $(3,1)$ یا $(3,-1)$ برود که به دزد نزدیک‌تر است. از آن‌جایی که دزد در نقطه‌ی $(5,1)$ قرار دارد قبل از اینکه حرکت کند دستگیر می‌شود.

پس نقطه‌ی $(5,1)$ یکی از نقاط دستگیری دزد است. با توجه به حالت‌های مختلف برای تصمیم‌گیری حرکت دزد،‌ همه‌ی نقاط قرمز مشخص شده در شکل بالا ممکن است محل دستگیری دزد باشد.

توضیح نمونه ۳

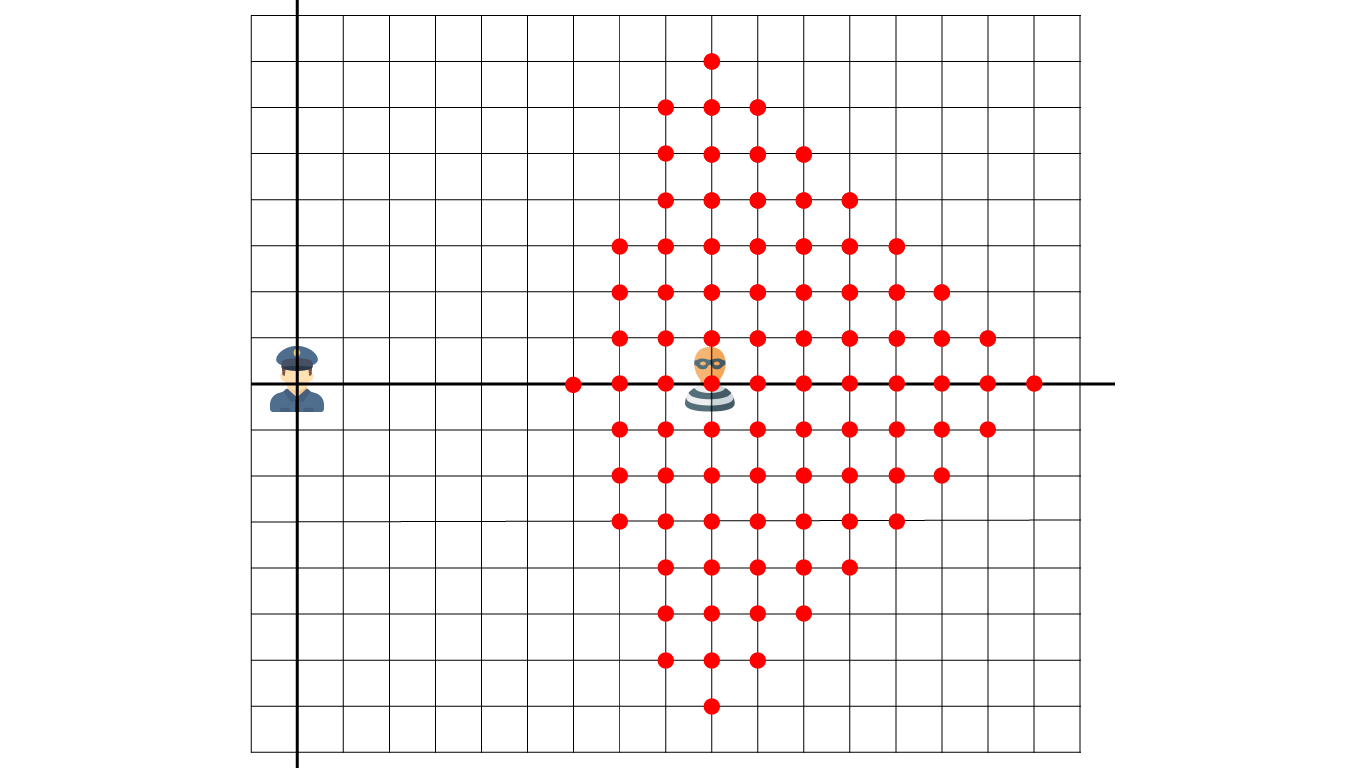
مشابه قبل همه‌ی نقاطی که محل دستگیری دزد هستند در شکل بالا نشان داده شده.