- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
نقشهی کشور فانو مانند شکل زیر است. این کشور از ۷ شهر با شمارههای ۱ تا ۷ تشکیل شده است. بین این شهرها تعدادی جاده مستقیم و دو طرفه وجود دارد.
در یک روز متوجه میشویم که دزدی در شهر $r$ وجود دارد و پلیس این کشور در شهر $c$ مشغول خدمت رسانی است. بازی دزد و پلیس شروع میشود.

در این بازی، روزها پلیس و شبها دزد حرکت میکند. هر کس در زمان حرکت، یکی از جادههای خارج شده از شهر خودش را انتخاب میکند و به شهر مجاور میرود.
از صبح روز اول این بازی شروع میشود و این کار تا زمانی که پلیس به شهری که دزد در آن قرار دارد برسد و او را دستگیر کند، ادامه پیدا میکند.
فرض کنید هر دوی دزد و پلیس هوشمندانهترین حرکت ممکن را انجام میدهند. یعنی دزد به شهری میرود که در دیرترین زمان ممکن دستگیر شود و پلیس به شهری میرود که در زودترین زمان ممکن دزد را دستگیر کند. پلیس و دزد همیشه جای یکدیگر را میدانند.
حال از شما میخواهیم کمترین تعداد روزی که باید بگذرد تا دزد دستگیر شود را چاپ کنید و یا اعلام کنید دزد هیچوقت دستگیر نمیشود.
ورودی
در سطر اول ورودی، عدد صحیح $c$ آمده که شمارهی شهری که پلیس در آن قرار دارد را نشان میدهد. در سطر دوم ورودی، عدد صحیح $r$ آمده که شمارهی شهری که دزد در آن قرار دارد را نشان میدهد.
$$1 \leq r \neq c \leq 7$$
خروجی
در تنها سطر خروجی، یک عدد صحیح که برابر کمترین تعداد روزی که باید بگذرد، تا پلیس، دزد را بگیرد را چاپ کنید. اگر دزد هیچوقت توسط پلیس دستگیر نمیشود -1 چاپ کنید.
مثالها
ورودی نمونه ۱
2
6
خروجی نمونه ۱
1

در این نمونه، پلیس روز اول، از شهر ۲ وارد شهر ۶ میشود و دزد را دستگیر میکند.
ورودی نمونه ۲
7
1
خروجی نمونه ۲
2
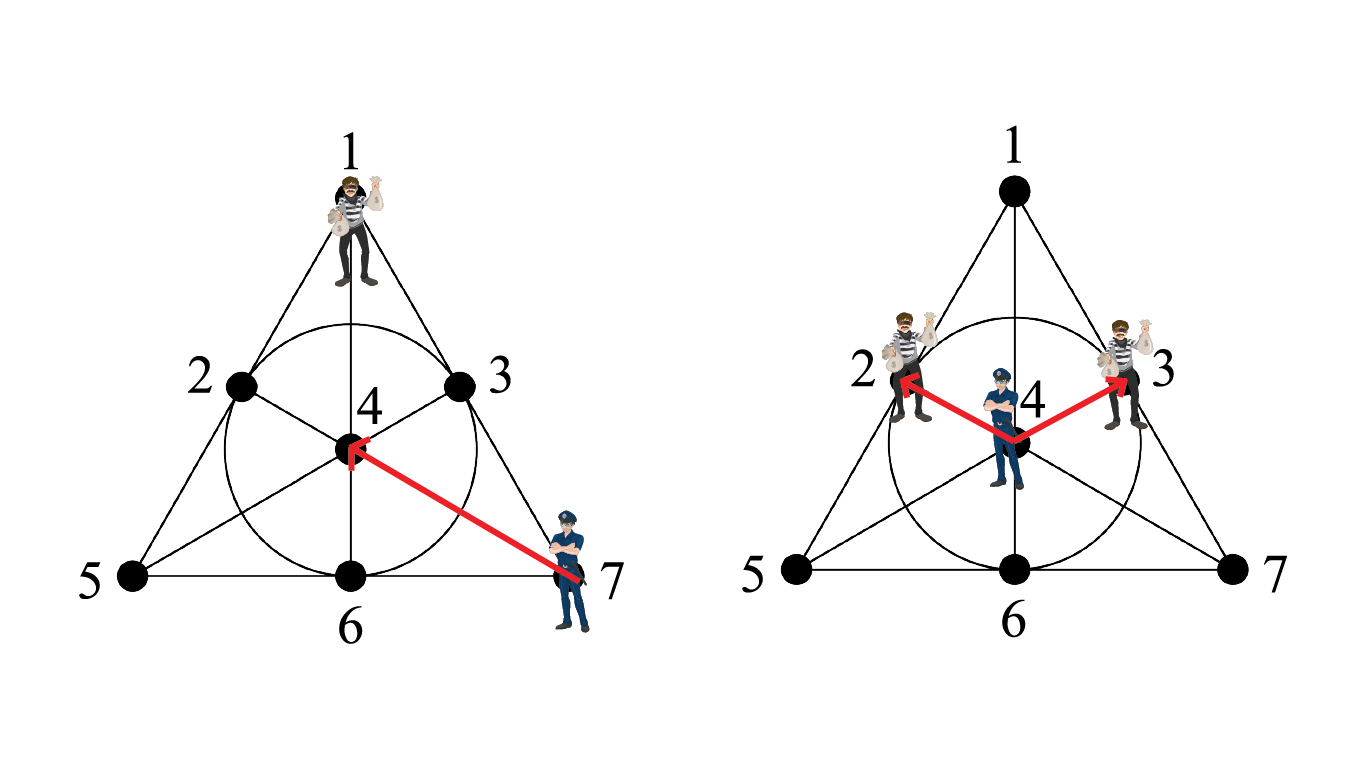
در این نمونه، پلیس روز اول، از شهر ۷ وارد شهر ۴ میشود. شب اول دزد به یکی از شهرهای ۲ یا ۳ میرود و در هر کدام از این شهرها که باشد، پلیس روز دوم آن را دستگیر میکند.
ورودی نمونه ۳
4
7
خروجی نمونه ۳
1

در این نمونه، پلیس روز اول، از شهر ۴ وارد شهر ۷ میشود و دزد را دستگیر میکند.
ارسال پاسخ برای این سؤال