• محدودیت زمان: ۴ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

استاد که سخت مشغول طرح سوال برای المپیک فناوری است، فرصت برای طراحی لوگو المپیک فناوری ندارد. او برای زدن ۷ ۸ تیر با یک نشان، از همین موضوع نیز سوال طرح کرده است!

او در هر پرسش به شما $n$ بازه‌ی بسته $[l_1, r_1], [l_2, r_2], \dots [l_n, r_n]$ می‌دهد که زیبایی بازه $i$ام برابر $s_i$ است و می‌پرسد که بیشینه زیبایی ۵-تایی المپیکی که با این بازه‌ها می‌توان ساخت، چیست.

به ۵ بازه‌ی $(a, b, c, d, e)$ ۵-تایی المپیکی گوییم، هرگاه:

• $l_a < l_b < r_a < r_b$
• $l_d < l_e < r_d < r_e$
• $l_c < r_b < l_d < r_c$

زیبایی یک ۵-تایی المپیکی برابر با مجموعه زیبایی ۵ بازه‌ی آن است.

ورودی

در خط اول ورودی عدد صحیح $t$ که برابر تعداد پرسش‌ها است، می‌آید. $$1 \le t \le 100,000$$

در خط اول هر پرسش، عدد صحیح $n$ که برابر تعداد بازه‌ها در آن پرسش است، می‌آید. $$1 \le n \le 500,000$$

در خط $i$ام از $n$ خط بعدی، سه عدد صحیح $l_i$ و $ r_i$ و $s_i$ که به ترتیب نشان‌دهنده‌ی سر و ته و زیبایی بازه‌ی $i$ام هستند، می‌آیند.

$$1 \le l_i \le r_i \le 500,000$$ $$1 \le s_i \le 1,000,000$$

تضمین می‌شود که مجموع $n$ها در همه‌ی پرسش‌ها حداکثر برابر $500,000$ است.

خروجی

برای هر پرسش، در صورتی که هیچ مجموعه‌ی المپیکی‌ای وجود ندارد عدد $-1$ و در غیر این صورت، بیشینه‌ی زیبایی یک ۵-تایی المپیکی را خروجی دهید.

مثال

ورودی نمونه ۱

2
5
1 3 1
2 4 2
3 6 3
5 7 4
6 8 5
5
1 3 10
2 4 10
3 5 10
5 7 10
6 8 10

خروجی نمونه ۱

15
-1

در پرسش اول، بازه‌های $(1, 2, 3, 4, 5)$ تشکیل یک ۵-تایی المپیکی می‌دهند. هیچ ۵-تایی المپیکی دیگری در این پرسش وجود ندارد.

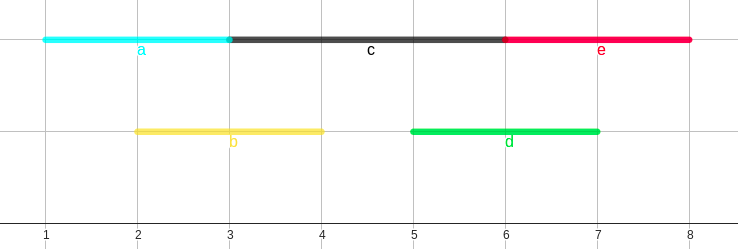بازه‌های پرسش اول - دقت کنید که بعد عمودی نقاط صرفا برای وضوح شکل است.

در پرسش دوم، هیچ ۵-تایی المپیکی‌ای وجود ندارد.

ورودی نمونه ۲

1
8
1 4 7
2 5 6
3 6 3
4 7 5
5 8 2
6 9 9
7 10 4
8 11 5

خروجی نمونه ۲

32

در تنها پرسش این مثال، ۵-تایی $(1, 2, 4, 6, 8)$ بیشترین امتیاز را در میان ۵-تایی‌های المپیکی دارد.