• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت
• منبع: آزمون مقدماتی اول دوره ۲۶ المپیاد کامپیوتر

---

توابع \(f: \mathbb{N} \rightarrow \{-1, 1\}\) و \(g: \mathbb{N} \rightarrow \mathbb{Z}\) به صورت زیر تعریف می‌شوند:

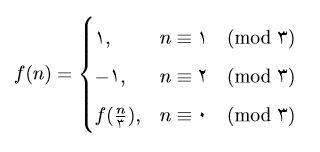
\[g(n)=\sum_{i=1}^{n}f(i)\]

در توضیحات بالا، منظور از \(\mathbb{N}\) مجموعه‌ی اعداد طبیعی و منظور از \(\mathbb{Z}\) مجموعه‌ی اعداد صحیح است.

برنامه‌ای بنویسید که \(q\) پرسمان به صورت \((l,r)\) دریافت کند و به ازای هر پرسمان تعداد نابجایی‌های دنباله‌ی \(g(l), g(l+1), \ldots, g(r)\) را محاسبه کند. با توجه به این‌که پاسخ پرسمان‌ها می‌تواند بزرگ باشد، باقی‌مانده‌ی آن بر \(10^9 + 7\) را محاسبه کنید.

تعداد نابجایی‌های دنباله‌ی \(a_1, a_2, \ldots, a_n\) برابر است با تعداد جفت \((i,j)\) هایی که \(i < j\) و \(a_i > a_j\) است.

ورودی

در سطر اول ورودی عدد طبیعی \(q\)، تعداد پرسمان‌ها، آمده است.

در هر یک از \(q\) سطر بعدی به ترتیب دو عدد طبیعی \(l\) و \(r\) آمده است.

\[1\leq q\leq 50\ 000\] \[1\leq l \leq r\leq 10^{18}\]

خروجی

خروجی شامل \(q\) سطر است که در \(i\) امین \((1\leq i\leq q)\) سطر از آن، پاسخ پرسمان \(i\) ام آمده است.

زیرمسئله‌ها

زیرمسئله	نمره	محدودیت
۱	۲۵	\(l,r \leq 1\ 000\ 000\)
۲	۲۵	\(r - l \leq 100, q \leq 10\ 000\)
۳	۵۰	بدون محدودیت اضافی

مثال

ورودی نمونه ۱

4
1 1
2 3
1 5
3 17

خروجی نمونه ۱

0
0
2
25