• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

یک گراف (جهت‌دار یا بدون جهت) به همراه یک راس مبدا و یک راس مقصد به شما داده می‌شود و از شما خواسته می‌شود تمام مسیر‌های از مبدا تا مقصد که طولشان در بازه‌ی مشخصی قرار دارد، را بیابید. سپس تعداد و شناسه‌ی تمام یال‌های موجود در این مسیر‌ها را در خروجی چاپ کنید.

نکات مهم:

1. جهت‌دار یا بدون جهت بودن گراف در ورودی مشخص می‌شود (در صورتی که گراف جهت‌دار باشد، جهت یال‌ها باید هم‌جهت با مسیر باشد و در صورت بدون جهت بودن گراف جهت یال‌ها هیچ اهمیتی ندارد).
2. کمترین و بیشترین طول مسیر مجاز در ورودی ذکر می‌شود.
3. هر یال گراف شامل سه عدد برای شناسه‌ی یال، شماره‌ی راس اول و شماره‌ی راس دوم است. (شناسه یال‌ها از هم متمایز هستند.)
4. در یک مسیر مجاز، از یک یال یا راس دو بار عبور نمی‌کنیم. (در یک مسیر مجاز دور نداریم.)

ورودی

1. در خط اول ورودی $n$ (تعداد راس‌های گراف) و $m$ (تعداد یال‌های گراف) با یک فاصله از هم وارد می‌شود. (تمامی راس‌های گراف از ۱ تا $n$ شماره گذاری می‌شوند.)
2. در خط دوم $s$ (شماره‌ی راس مبدا) و $t$ (شماره‌ی راس مقصد) وارد می‌شوند.
3. در خط سوم $min$ (کمترین طول مسیر) و $max$ (بیشترین طول مسیر) وارد می‌شود.
4. در خط چهارم ورودی $d$ (جهت‌دار بودن یا بدون جهت بودن گراف) وارد می‌شود. در صورتی که ۱ باشد، گراف جهت‌دار است و در صورتی که ۰ باشد، گراف بدون جهت است.
5. سپس در $m$ خط بعدی در هر خط اطلاعات یکی از یال‌های گراف وارد می‌شود. اطلاعات هر یال شامل سه عدد برای شناسه‌ی یال، شماره‌ی راس اول و دوم (برای گراف‌های جهت‌دار راس اول مبدا و راس دوم مقصد) خواهد بود.

$$1 \le n \le 1\ 000 $$ $$1 \le m \le 5 * n$$ $$1 \le s, t \le n$$ $$ 1 \le min, max \le 8 $$ $$ min \le max $$

خروجی

در خط اول خروجی تعداد تمام یال‌هایی که در مسیرهایی به کمترین و بیشترین طول داده شده وجود دارند نمایش داده می‌شوند. در خط دوم خروجی شناسه‌ی تمام یال‌های مذکور به ترتیب (از کوچک به بزرگ) با یک فاصله از هم نمایش داده می‌شوند.

مثال

ورودی نمونه ۱

3 4
1 2
2 4
0
1 1 2
2 2 3
3 1 3
4 3 1

خروجی نمونه ۱

3
2 3 4

توضیحات نمونه‌ی ۱

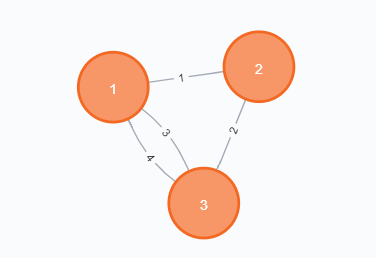
با توجه به جدول زیر تعداد مسیر به حداقل طول ۲ و حداکثر طول ۴، ۲ تاست و یال‌های ۲، ۳ و ۴ در آن وجود دارند. بنابراین عدد ۳ (تعداد یال‌ها) و شناسه‌ی یال‌ها در خروجی چاپ می‌شود.

	یال‌های موجود
مسیر ۱	۳ ۲
مسیر ۲	۴ ۲

ورودی نمونه ۲

5 6
1 3
2 5
1
1 2 1
2 2 3
3 1 3
4 1 4
5 5 4
6 5 3

خروجی نمونه ۲

0

توضیحات نمونه‌ی ۲

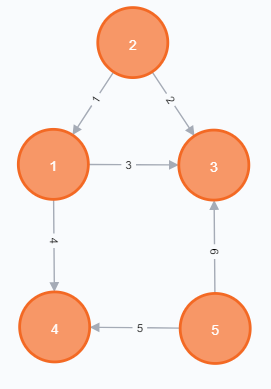
با توجه به جهت‌دار بودن گراف هیچ مسیری از مبدا (راس ۱) به مقصد (راس ۳) به حداقل طول ۲ و حداکثر طول ۵، وجود ندارد. بنابراین عدد ۰ در خروجی چاپ می‌شود.