• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۶۴ مگابایت

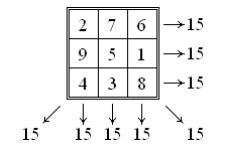
یک مربع جادویی، یک ماتریس $n \times n$ است که در آن، عداد $m$ تا $m + n^2 - 1$ قرار دارند و مجموع اعداد هر سطر، هر ستون و هر قطر، باهم برابر است. شکل زیر یک مربع جادویی $3 \times 3$ را نشان می‌دهد که در آن اعداد یک تا ۹ قرار گرفته‌اند و مجموع اعداد هر سطر، ستن و قطر برابر با ۱۵ است.

یک راه حل برای ساختن مربع جادویی از مرتبه‌ی فرد (وقتی که $n$ فرد باشد)، قرار دادن کمینه‌ی اعداد $m$ در خانه‌ی شماره $\frac{n+1}{2}$ از ردیف اول و سپس شروع به قراردهی اعداد از عدد $k = m + 1$ مطابق الگوریتم زیر است. توجه شود که بالاترین سطر شماره یک، پایین‌ترین سطر شماره $n$، چپ‌ترین ستون شماره یک و راست‌ترین ستون شماره $n$ فرض شده است.

1. به سمت راست-بالا حرکت کن؛ بنابراین اگر خانه‌ی فعلی سطر $i$ و ستون $j$ باشد، خانه‌ی بعدی سطر $i-1$ و ستون $j+1$ خواهد بود.

2. اگر شماره‌ی سطر و شماره‌ی ستون خانه از یک تا $n$ باشد، به مرحله‌ی شماره ۳ برو. در غیر این صورت، چنانچه شماره‌ی سطر صفر باشد، شماره‌ی سطر را به $n$ تغییر بده و در صورتی که شماره ستون $n+1$ باشد، آن را به شماره‌ی یک تغییر بده.

3. چنانچه خانه قبلاً توسط عددی پر شده باشد، شماره‌ی سطر را یک عدد افزایش بده (یک ردیف یه پایین بیا)؛ در غیر این صورت به مرحله‌ی ۴ برو.

4. عدد $k$ را در خانه قرار بده. اگر تمامی خانه‌ها پر باشد، مربع جادویی ساخته‌شده است؛ در غیر این صورت عدد را یکی افزایش بده و مرحله‌ی یک را تکرار کن.

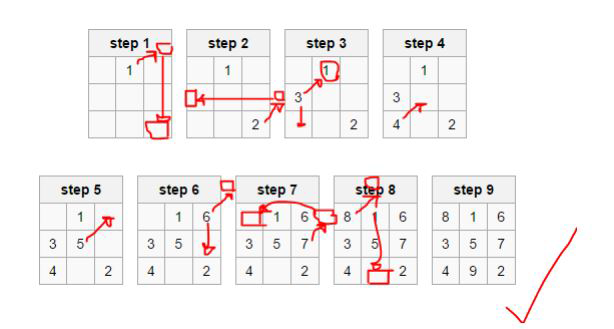
در شکل زیر، $m$ برابر یا یک و $n$ برابر با سه است. مراحل این الگوریتم به ترتیب مشاهده می‌شود. همانطور که می‌بینید، خروجی الگوریتم، مربعی جادویی است مجموع هر سطر، ستون و یا قطر آن برابر با ۱۵ است. حال برنامه‌ای بنویسید که ابتدا عدد $n$ و سپس عدد $m$ گفته شده در بالا را دریافت کند و مطابق با الگوریتم گفته شده، مربع جادویی را تولید کند.

ورودی

در ورودی عدد $n$ و $m$ آمده است. $$1 \leq n , m \leq 1\ 000$$

خروجی

در خروجی مربع جادویی را چاپ کنید.

مثال

ورودی نمونه ۱

3 1

خروجی نمونه ۱

8 1 6
3 5 7
4 9 2