• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

Everland and Neverland are two neighboring countries, and a huge number of Everlandian tourists visit Neverland every year. The governments want to analyze the passport control process in the border of Neverland and Everland, and need your help!

In the border, tourists stand in $q$ queues for their passport check, and there are $q + 1$ passport control gates. If we number the gates from $0$ to $q$ and number the queues from $0$ to $q - 1$, the tourists standing in queue $i$ can only pass through gates $i$ or $i + 1$.

Whenever gate $i$ opens, if one of the queues $i$ and $i - 1$ is empty or non-existent, the tourist at the front of the other queue passes through the gate. If both queues $i$ and $i - 1$ are non-empty, the older tourist between the ones at the front of two queues passes through the gate. It is assumed that no two gates open at the same time.

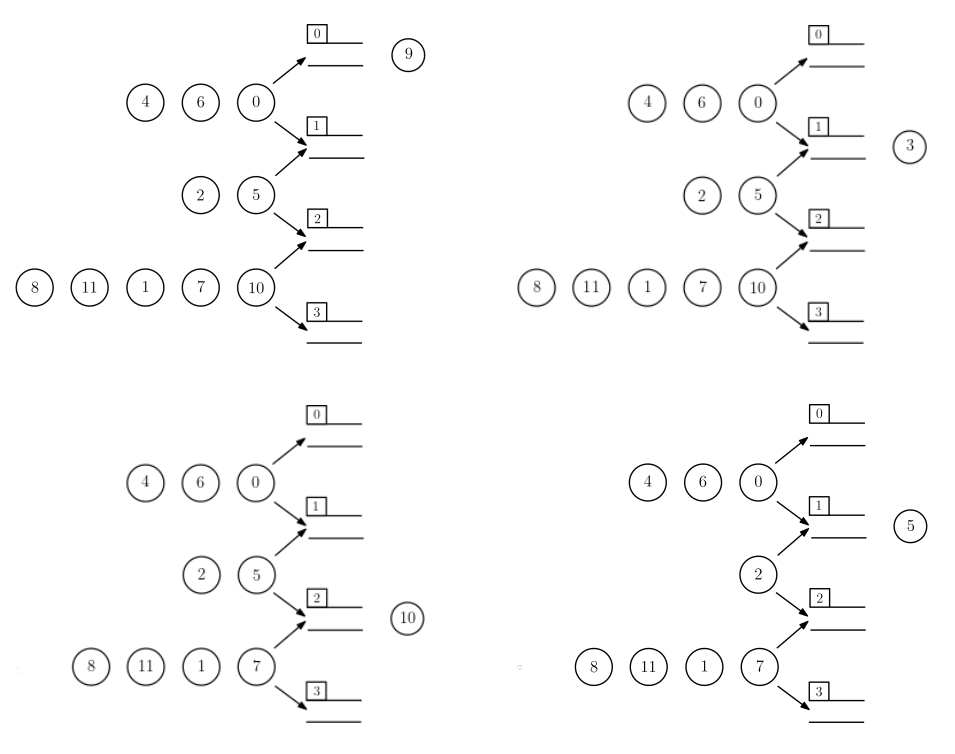
We have a picture of $n$ tourists standing in queues; waiting for the gates to open. Also, we have another picture that has been taken a while later, that some of the tourists from the first picture have passed through the gates. The tourists in the pictures are numbered from $0$ to $n-1$, in the order of their ages such that the person number $0$ is the youngest and the person number $n-1$ is the oldest. The picture below shows the first four configurations of the tourists in the first sample.

You are asked to find any valid sequence of gates’ opening that might have happened between the times the two pictures were taken, or claim that it is impossible. A gate can be opened multiple times in the sequence.

ورودی

The first line of the input contains two integers $q$ ($1 \leq q \leq 100, 000$), the number of queues, and $n$ ($0 \leq n \leq 100, 000$), the number of tourists in the first picture. The $i$-th line of the next following $q$ lines describes queue $i - 1$ in the first picture. Each queue description starts with a number $k$ ($0 \leq k \leq n$) that shows the size of the queue, followed by $k$ integers that indicate the tourist numbers in that queue, from the back to the front. The tourist numbers are unique and non-negative integers less than $n$. In the next following $q$ lines the description of the second picture appears in the same format.

خروجی

If there is no valid sequence, print Impossible. If there are valid sequences, output any of them in the following format. Print the length of the sequence in the first line and the sequence itself in the second line. In your sequence, every time any gate opens, there must be at least one tourist waiting for it.

مثال

ورودی نمونه ۱

3 12
4 4 6 0 9
3 2 5 3
5 8 11 1 7 10
3 4 6 0
1 2
2 8 11

خروجی نمونه ۱

6
0 1 2 1 2 3

ورودی نمونه ۲

3 3
1 2
1 0
1 1
1 2
0
1 1

خروجی نمونه ۲

Impossible

ورودی نمونه ۳

1 2
2 0 1
2 1 0

خروجی نمونه ۳

Impossible

ورودی نمونه ۴

1 2
2 0 1
2 0 1

خروجی نمونه ۴

0