• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

عمو اسکروچ که آدم سنگینی است، برای اینکه سنگینی خودش را به دوستان خود اثبات کند، تصمیم گرفت که یک مسئله‌ی گراف را برای آنها حل کند. ولی از آنجا که او علاوه بر سنگین بودن، حق‌گویی پایینی دارد از شما کمک می‌خواهد تا مسئله را برای او حل کنید:

یک گراف ساده‌ی $n$ رأسی داریم. سنگینی یک مسیر را برابر با XOR اعداد روی یال‌های آن در نظر می‌گیریم. تابع $f$ را برای دو رأس $v$ و $u$ برابر با بیشترین مقدار سنگینی بین تمام مسیرهای ساده بین دو رأس $v$ و $u$ قرار می‌دهیم (در صورتی که بین این دو رأس مسیری نباشد، برابر با صفر قرار می‌دهیم). می‌خواهیم روی یال‌های گراف اعداد ۰ یا ۱ بنویسیم به طوری مقدار زیر بیشینه شود: $$\sum_{v < u \in V \left (G \right)}f\left(v, u\right)$$ بیشینه مقدار این عبارت را خروجی دهید.

ورودی

در خط اول ورودی، دو عدد طبیعی $n$ و $m$ با فاصله از هم آمده است که به ترتیب نشان دهنده‌ی تعداد رئوس و یال‌های گراف است. در ادامه، $m$ خط آمده است و در خط $i$ اًم، دو عدد $v_i$ و $u_i$ آمده است که نشان دهنده‌ی یک یال، بین این دو رأس است. $$3 \le n \le 100\ 000$$ $$1 \le m \le 200\ 000$$$$1 \le v_i, u_i \le n$$

خروجی

در تنها خط خروجی، جواب مسئله را چاپ کنید.

مثال

ورودی نمونه ۱

4 4
1 2
2 3
3 4
4 1

خروجی نمونه ۱

6

اگر روی یال $(2, 1)$ عدد ۱، و روی باقی یال‌ها عدد ۰ بنویسیم، گرافی به شکل زیر خواهیم داشت:

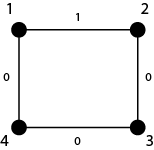
در این صورت مقادیر مختلف $f$ به شکل زیر خواهد بود:
مقدار تابع به ازای رأس‌های ۱ و ۲ برابر ۱ خواهد بود، زیرا می‌توان مسیر $1\to2$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۱ و ۳ برابر ۱ خواهد بود، زیرا می‌توان مسیر $1\to2\to3$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۱ و ۴ برابر ۱ خواهد بود، زیرا می‌توان مسیر $1\to2\to3\to4$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۲ و ۳ برابر ۱ خواهد بود، زیرا می‌توان مسیر $2\to1\to4\to3$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۲ و ۴ برابر ۱ خواهد بود، زیرا می‌توان مسیر $2\to1\to4$ را انتخاب کرد.
مقدار تابع به ازای رأس‌های ۳ و ۴ برابر ۱ خواهد بود، زیرا می‌توان مسیر $3\to2\to1\to4$ را انتخاب کرد.

ورودی نمونه ۲

5 4
1 2
2 3
3 1
4 5

خروجی نمونه ۲

4