• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت
• منبع: آزمون نهایی دوم دوره ۲۶ المپیاد کامپیوتر

---

برادران دالتون پس از فرار از زندان برای تامین مخارج روزمره‌ی زندگی به استخراج از چاه‌های نفت دوبعدی روآورده اند. یک چاه نفت دوبعدی به شکل یک جدول نامتناهی با $n$ ستون و $10^9$ سطر است که در بالای سطر اول آن، سطح زمین قرار گرفته است. هر ستون از میزان‌های مشخصی از خاک، نفت و سنگ تشکیل شده است. بر اساس نحوه‌ی به وجود آمدن نفت طی مرور زمان، در هر ستون از چاه نفت، در یک بازه‌ی صحیحی از عمق زمین نفت وجود دارد که این بازه را برای ستون $i$ام با $[l_i, r_i]$ نشان می‌دهیم و به این معناست که از عمق $l_i$ تا عمق $r_i$ از ستون $i$ام از نفت تشکیل شده است. درنتیجه این ستون شامل $r_i - l_i$ واحد نفت است. هم‌چنین می‌دانیم که همواره از سطح زمین تا عمق شروع نفت، یعنی بازه‌ی $[0, l_i]$، از خاک تشکیل شده، و از عمق پایان نفت تا انتهای چاه نفت، یعنی بازه‌ی $[r_i, 10^9]$، از سنگ تشکیل شده است. برای مثال، اگر بازه‌ی نفت در یک ستون $[1,3]$ باشد، در آن ستون، ۱ واحد خاک و ۲ واحد نفت موجود است.

برادران دالتون‌ که برای استخراج نفت از چاه‌ها وقت زیادی ندارند، برای استخراج نفت به این شکل عمل می‌کنند که دقیقاً تعدادی ستون متوالی را انتخاب کرده و تا عمق مشخصی با استفاده از دستگاه نفت‌کَن، زمین را می‌کَنند. در صورتی که در زیرمستطیلی از چاه نفت که دستگاه نفت‌کَن می‌کَند حتا یک واحد سنگ موجود باشد، دستگاه خراب می‌شود و به همین خاطر برادران دالتون نمی‌خواهند در زیر مستطیلی که می‌کَنند سنگ وجود داشته باشد. پس از کندن یک زیرمستطیل از چاه نفت تمامی واحد‌های خاک آن نابود می‌شوند ولی تمامی واحدهای نفت موجود در آن از خروجی دستگاه نفت‌کَن بیرون می‌آید و برادران دالتون آن‌ها را جمع‌آوری می‌کنند.

پس از کندن یک زیرمستطیل از چاه نفت، برادران دالتون می‌توانند از تمامی منافذی که به ذخایر نفت متصل است، با استفاده از دستگاه نفت‌کِش، نفت استخراج کنند. دقت‌کنید که منظور از منافذ تمام درایه‌هایی شامل نفت از ماتریس است که پس از کَندن زیرمستطیل در معرض هوا قرار گرفته اند. به عبارت دیگر، تمام درایه‌های موجود در جدول که یکی از درایه‌های مجاور (منظور از مجاورت در این سوال، مجاورت ضلعی است. به این معنی که دو درایه ضلع مشترک داشته باشند). آن‌ها درون ‌زیرمستطیل کنده شده قرار داشته است. دستگاه نفت‌کِش پس از اتصال به یک منفذ، تمامی واحد‌های نفت که با مسیری از درایه‌های شامل نفت به منفذ می‌رسد را می‌مکد و از خروجی بیرون می‌دهد تا برادران دالتون آن‌ها را جمع آوری کنند. یک درایه‌ی شامل نفت به یک منفذ مسیر دارد، اگر دنباله‌ای از درایه‌های شامل نفت با شروع از آن خانه و پایان در منفذ موجود باشد که هر دو عضو متوالی در دنباله مجاور باشند.

حداکثر مقدار نفتی که برادران دالتون می‌توانند جمع کنند چقدر است؟

ورودی

در خط اول ورودی $n$، تعداد ستون‌های چاه نفت آمده است. در $n$ خط بعدی ورودی،‌ در هر خط دو عدد طبیعی $l_i$ و $r_i$ آمده است که شروع و پایان بازه‌ی تشکیل شده از نفت در ستون $i$ام را نشان می‌دهند. $$1 \le n \le 200\ 000$$ $$1 \le l_i \le r_i \le 10^9$$

خروجی

در تنها خط خروجی، حداکثر مقدار نفتی که برادران دالتون می‌توانند جمع کنند را چاپ کنید.

زیرمسئله‌ها

زیرمسئله	نمره	محدودیت
۱	۱	نفت نداریم ($l_i = r_i$)
۲	۲	سنگ نداریم ($r_i = 10^9$)
۳	۳	خاک نداریم ($l_i = 1$)
۴	۱۲	$n \le 20$
۵	۲۱	$n \le 2\ 000$
۶	۶۱	بدون محدودیت اضافی

دقت کنید همواره یک لایه خاک بر روی چاه نفت وجود دارد و در زیرمساله‌ی سوم منظور بدون درنظر گرفتن آن لایه است.

مثال

ورودی نمونه ۱

11
2 2
2 4
3 4
3 3
4 5
4 5
3 4
3 5
4 6
3 5
1 2

خروجی نمونه ۱

11

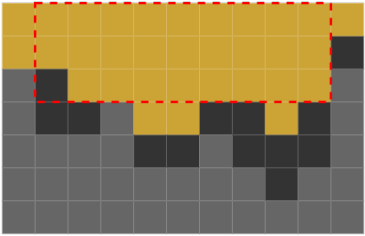
ورودی نمونه همان شکل صفحه‌ی اول سوال است و خط ‌چین قرمز زیرمستطیلی که نفت‌کَن می‌کَند را نشان می‌دهد.