---------- To guard the art jewelry exhibition at night, the security agency has decided to use a new laser beam system, consisting of sender-receiver pairs. Each pair generates a strip of light of one unit width and guards all objects located inside the strip. Your task is to help the agency and to compute for each exhibition room the minimum number of sender-receiver pairs which are sufficient to protect all exhibits inside the room. Any room has a rectangle shape, so we describe it as an $[0, N] × [0, M]$ rectangle in the plane. The objects we need to guard are represented as points inside that rectangle. Each sender is mounted on a wall and the corresponding receiver on the opposite wall in such a way that the generated strip is a rectangle of unit width and length either $N$ or $M$. Since the new laser beam system is still not perfect, each sender-receiver pair can only be mounted to generate strips the corners of which have integer coordinates. An additional drawback is that the sender-receiver pairs can protect only items inside the strips, but not those lying on their borders. Thus, the security agency arranged the exhibits in such a way that both coordinates of any point representing an exhibit are non-integers. 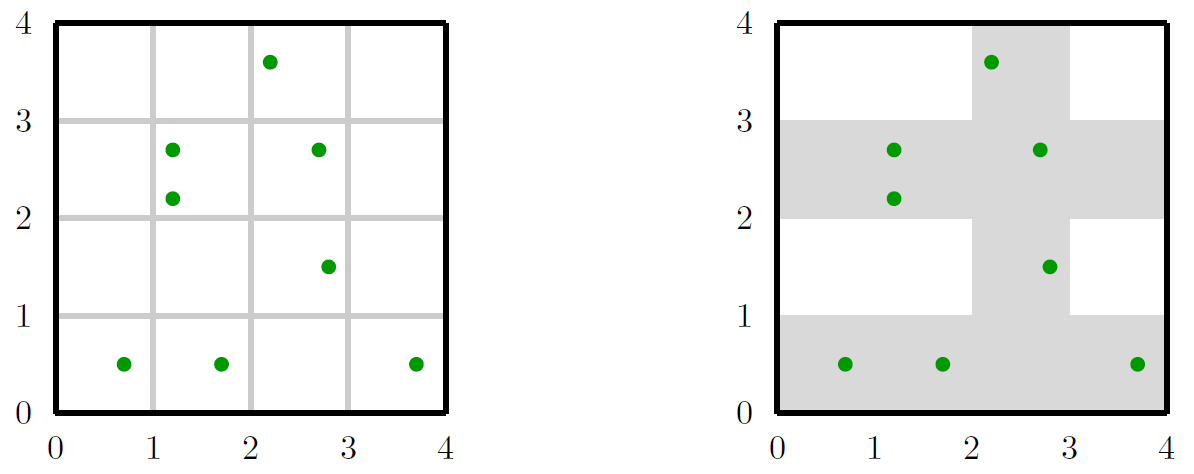The figure below (left) illustrates eight items arranged in $[0, 4] × [0, 4]$ (the second sample input). In the room, up to eight sender-receiver pairs can be mounted. The figure to the right shows an area protected by three sender-receiver pairs.  # Input The input starts with the number of exhibition rooms $R \le 10$. Then the descriptions of the $R$ rooms follow. A single description starts with a single line, containing three integers: $0 < N \le 100$, $0 < M \le 100$, specifying the size of the current room and $0 < K \le 104$, for the number of exhibits. Next $K$ lines follow, each of which consists of two real numbers $x, y$ describing the exhibit coordinates. You can assume that $0 < x < N$, $0 < y < M$ and that $x$ and $y$ are non-integer. # Output For every room output one line containing one integer, that is the minimum number of sender-receiver pairs sufficient to protect all exhibits inside the room. ## Sample Input ``` 2 1 5 3 0.2 1.5 0.3 4.8 0.4 3.5 4 4 8 0.7 0.5 1.7 0.5 2.8 1.5 3.7 0.5 2.2 3.6 2.7 2.7 1.2 2.2 1.2 2.7 ``` ## Sample Output ``` 1 3 ```

حل سؤال در بانک سؤالات