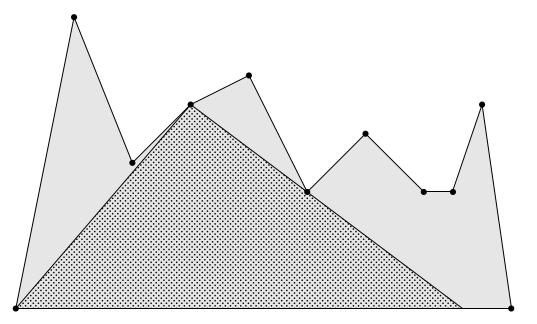
+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- A “terrain” is an $x$-monotone polygon defined by the points $p_1,\dots , p_n$ where each point $p_i$ has coordinates $(x_i, y_i)$, and the following three conditions hold: + $y_1 = y_n = 0$ + $y_i > 0$ for $1 < i < n$ + $x_i < x_{i+1}$ for $1 \leq i < n$  Given a terrain defined by the points $p_1, \dots , p_n$, find the largest triangle that fits entirely within the terrain, and one of its three vertices is positioned at one of the terrain points $p_2$ through $p_{n-1}$. # ورودی The first line of input contains an integer $n$, representing the number of points in the terrain $3 \leq n \leq 10^5$. The $i^{th}$ line in the following $n$ lines consists of two space-separated integers $x_i$ and $y_i$, representing the point $p_i$ of the terrain. $$0 \leq x_i, y_i \leq 10^9$$ # خروجی Print the area of the largest triangle contained within the terrain. Your output will be considered correct if its absolute or relative error is at most $10^{-6}$. # مثال ### ورودی نمونه ۱ ``` 11 0 0 2 10 4 5 6 7 8 8 10 4 12 6 14 4 15 4 16 7 17 0 ``` ### خروجی نمونه ۱ ``` 53.666667 ```

حل سؤال در بانک سؤالات