+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
There are many caves near Tehran, and Amin, after finishing this competition, wants to pick one of them to visit and leave competitions behind. The entrance to this cave looks like the following:
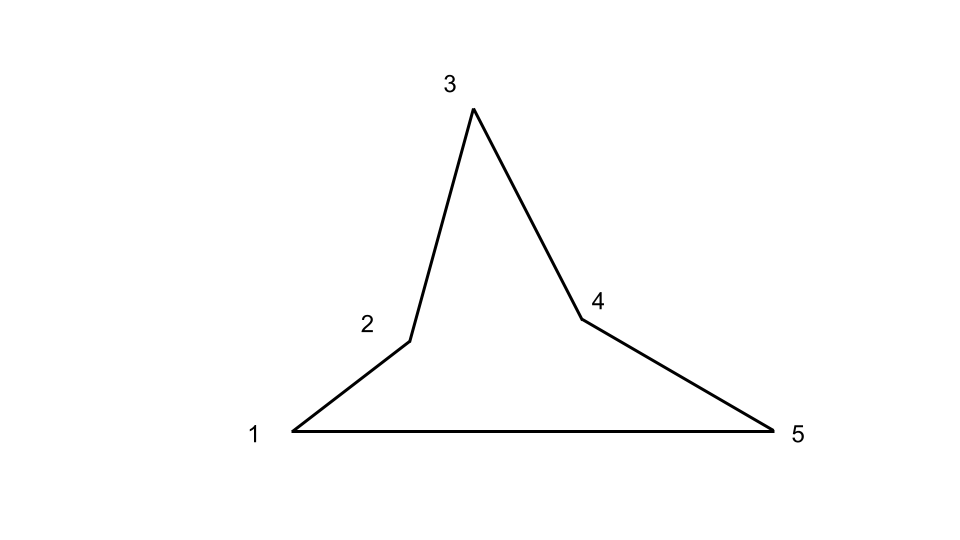
The cave entrance is shaped as an $n$-sided polygon in two dimensions. The entrance consists of two walls, left and right, each forming a concave curve.
The tops of both walls meet at a single point, while the bottoms connect with an straight line.
Amin wants to place a sensor on each vertex of this polygon. Each sensor can detect surroundings unless a wall blocks its view.
The entrance of the cave, as shown in an image, consists of two **concave** walls and a flat floor at the entrance.
There are $n$ sensors installed along the cave entrance, numbered from $1$ to $n$, starting from the bottom left and going to the bottom right.
Two sensors $i$ and $j$ can "see" each other if every point along the line between them lies within the cave space or along the boundary of the walls.
Based on this, we can construct an $n \times n$ table, where we write `1` in row $i$, column $j$ if sensor $i$ can see sensor $j$, and `0` otherwise.
Now, the problem reverses this process. Given an $n \times n$ table of `0`s and `1`s, determine if it's possible to find an arrangement of sensors along the cave entrance that matches the visibility pattern shown in the table.
# ورودی
The first line of input contains a positive integer $t$, representing the number of tables.
$$1 \leq t \leq 10^5$$
For each test case, The first line contains an integer $n$, representing the number of sensors.
$$3 \leq n \leq 100$$
The next $n$ lines each contain a string of length $n$, consisting of `0`s and `1`s, representing the table values.
$$\sum n \leq 10^5$$
# خروجی
For each test case, print `YES` if such an arrangement of sensors is possible, and `NO` otherwise.
# مثالها
## ورودی نمونه ۱
```
5
5
01011
10111
01010
11101
11010
4
0111
1011
1101
1110
3
000
000
000
4
0101
0101
1010
1010
3
111
101
110
````
## خروجی نمونه ۱
```
YES
NO
NO
NO
NO
````
J - Cave's Walls
ارسال پاسخ برای این سؤال
در حال حاضر شما دسترسی ندارید.
