- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
گز یک شهر نامتناهی است. خیابانهای این شهر به صورت زیر است.
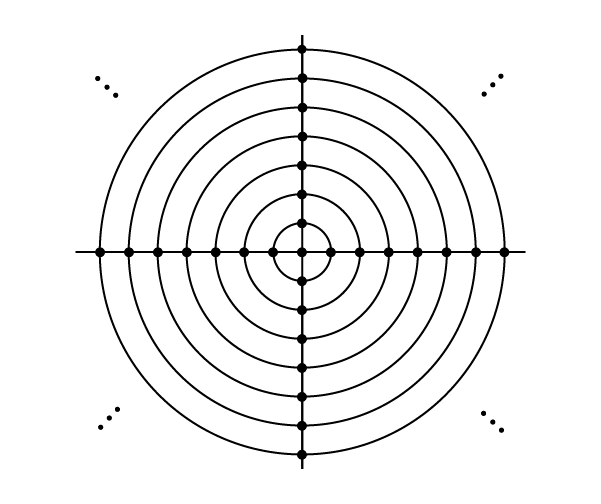
خیابانهای این شهر را میتوان روی صفحه مختصات دو بعدی به صورت زیر معرفی کرد.
- یک خیابان افقی منطبق بر محور $x$ها است.
- یک خیابان عمودی منطبق بر محور $y$ها است.
- به ازای هر عدد طبیعی مانند $n$، یک خیابان دایرهای به شعاع $n$ و مرکز مختصات وجود دارد.
میدانیم سعید در تقاطعی با مختصات $(x_1, y_1)$ و سجاد در تقاطعی با مختصات $(x_2, y_2)$ است.
سعید میخواهد بداند کمترین فاصلهای که باید در خیابانهای گز طی کند تا به سجاد برسد چقدر است.
ورودی
در سطر اول ورودی، عدد صحیح و مثبت $T$ آمده است که تعداد تستهای ورودی را نشان میدهد. $$1 \leq T \leq 100$$
در سطر اول هر، چهار عدد صحیح $x_1$، $y_1$، $x_2$ و $y_2$ که با یک فاصله از هم جدا شدهاند، آمده است؛ که نشاندهندهی مختصات تقاطع هایی است که سعید و سجاد در آن قرار دارند.
$$-10^9 \leq x_1, y_1, x_2, y_2 \leq 10^9$$
تضمین میشود که $(x_1, y_1)$ و $(x_2, y_2)$ مختصات دو تقاطع در شهر گز باشند.
خروجی
خروجی $t$ سطر دارد. در هر سطر، کمترین مسافتی که باید سعید طی کند تا به سجاد برسد را چاپ کنید.
باتوجه به اینکه پاسخ شما ممکن است عددی اعشاری باشد، زمانی عدد خروجی شما نمره کامل را دریافت میکند که با دقت حداقل ۳ رقم بعد از اعشار، پاسخ شما دقیق باشد.
مثالها
ورودی نمونه ۱
4
2 0 -4 0
0 3 5 0
0 -7 0 0
0 -5 0 -5
خروجی نمونه ۱
6.000000000000
6.712388980385
7.000000000000
0.000000000000
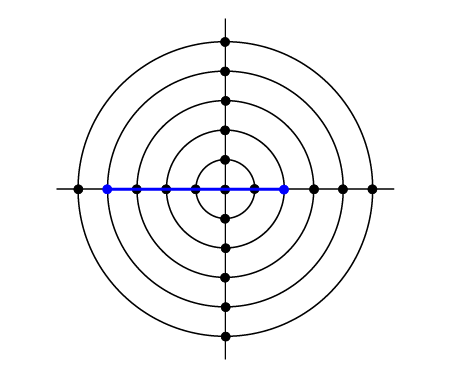
شکل تست اول.
کوتاهترین مسیر بین این دو تقاطع با یک جاده به شکل یک خط مستقیم است.
$$\sqrt{(2 - (-4))^2 + (0 - 0)^2} = 6$$
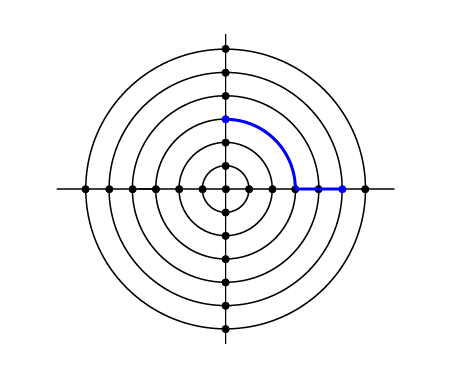
شکل تست دوم.
کوتاهترین مسیر بین این دو تقاطع با رنگ آبی مشخص شده است و طول آن برابر است با:
$$\frac{1}{4} \times (2\pi \times 3) + \sqrt{(5 - 3)^2 + (0 - 0)^2} = \frac{3\pi}{2} + 2 \approx 6.712388980385$$
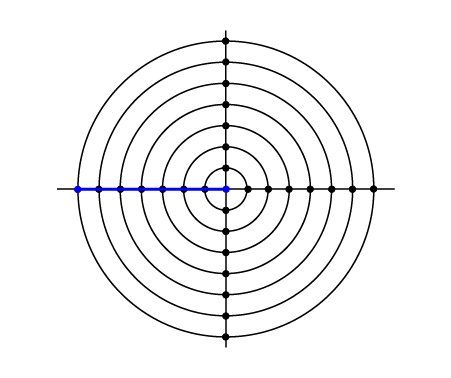
شکل تست سوم.
کوتاهترین مسیر بین این دو تقاطع با یک جاده به شکل یک خط مستقیم است. توجه کنید که مرکز شهر هم میتواند یک تقاطع باشد.
$$\sqrt{(-7 - 0)^2 + (0 - 0)^2} = 7$$
شکل تست چهارم.
کوتاهترین مسیر بین این دو تقاطع صفر در نظر گرفته میشود. چون این دو تقاطع برهم منطبق هستند.
$$0$$

ارسال پاسخ برای این سؤال