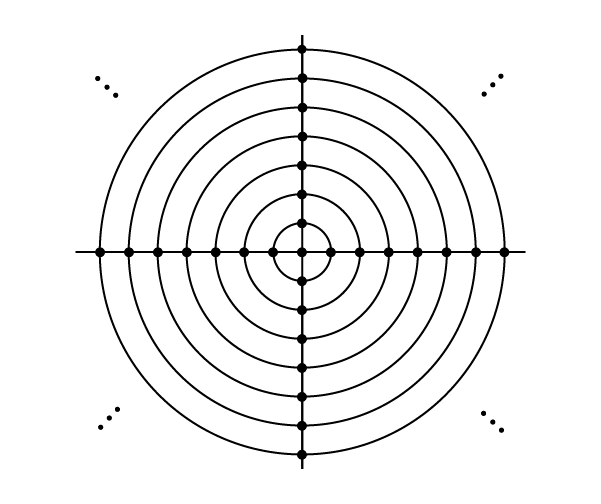
+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- *گز* یک شهر نامتناهی است. خیابان‌های این شهر به صورت زیر است.  خیابان‌های این شهر را می‌توان روی صفحه مختصات دو بعدی به صورت زیر معرفی کرد. + یک خیابان افقی منطبق بر محور $x$ها است. + یک خیابان عمودی منطبق بر محور $y$ها است. + به ازای هر عدد طبیعی مانند $n$، یک خیابان دایره‌ای به شعاع $n$ و مرکز مختصات وجود دارد. می‌دانیم *سعید* در تقاطعی با مختصات $(x_1, y_1)$ و *سجاد* در تقاطعی با مختصات $(x_2, y_2)$ است. *سعید* می‌خواهد بداند کمترین فاصله‌ای که باید در خیابان‌های گز طی کند تا به *سجاد* برسد چقدر است. # ورودی در سطر اول ورودی، عدد صحیح و مثبت $T$ آمده است که تعداد تست‌های ورودی را نشان می‌دهد. $$1 \leq T \leq 100$$ در سطر اول هر، چهار عدد صحیح $x_1$، $y_1$، $x_2$ و $y_2$ که با یک فاصله از هم جدا شده‌اند، آمده است؛ که نشان‌دهنده‌ی مختصات تقاطع هایی است که *سعید* و *سجاد* در آن قرار دارند. $$-10^9 \leq x_1, y_1, x_2, y_2 \leq 10^9$$ **تضمین می‌شود که $(x_1, y_1)$ و $(x_2, y_2)$ مختصات دو تقاطع در شهر *گز* باشند.** # خروجی خروجی $t$ سطر دارد. در هر سطر، کمترین مسافتی که باید *سعید* طی کند تا به *سجاد* برسد را چاپ کنید. 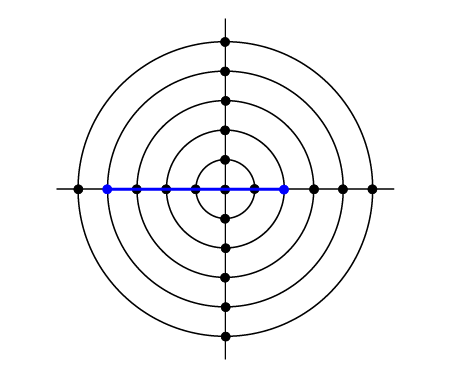**باتوجه به اینکه پاسخ شما ممکن است عددی اعشاری باشد، زمانی عدد خروجی شما نمره کامل را دریافت می‌کند که با دقت حداقل ۳ رقم بعد از اعشار، پاسخ شما دقیق باشد.** # مثال‌ها ## ورودی نمونه ۱ ``` 4 2 0 -4 0 0 3 5 0 0 -7 0 0 0 -5 0 -5 ``` ## خروجی نمونه ۱ ``` 6.000000000000 6.712388980385 7.000000000000 0.000000000000 ``` ---------- **شکل تست اول.** کوتاه‌ترین مسیر بین این دو تقاطع با یک جاده به شکل یک خط مستقیم است. 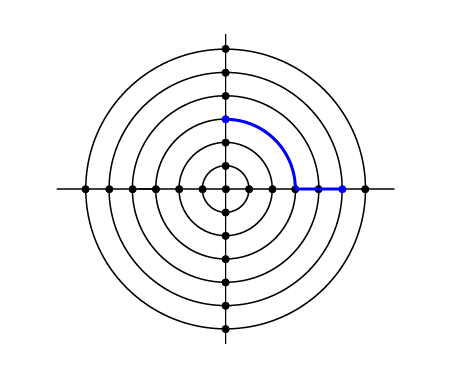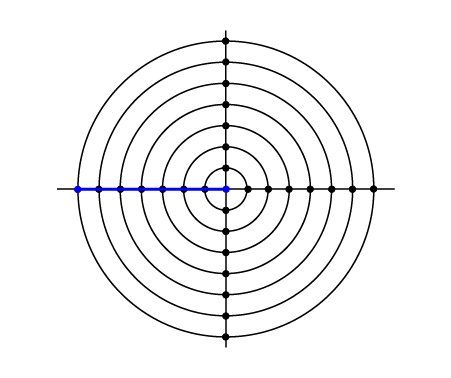$$\sqrt{(2 - (-4))^2 + (0 - 0)^2} = 6$$  ---------- **شکل تست دوم.** کوتاه‌ترین مسیر بین این دو تقاطع با رنگ آبی مشخص شده است و طول آن برابر است با: $$\frac{1}{4} \times (2\pi \times 3) + \sqrt{(5 - 3)^2 + (0 - 0)^2} = \frac{3\pi}{2} + 2 \approx 6.712388980385$$  ---------- **شکل تست سوم.** کوتاه‌ترین مسیر بین این دو تقاطع با یک جاده به شکل یک خط مستقیم است. توجه کنید که مرکز شهر هم می‌تواند یک تقاطع باشد. $$\sqrt{(-7 - 0)^2 + (0 - 0)^2} = 7$$  ---------- **شکل تست چهارم.** کوتاه‌ترین مسیر بین این دو تقاطع صفر در نظر گرفته می‌شود. چون این دو تقاطع برهم منطبق هستند. $$0$$ 

حل سؤال در بانک سؤالات