• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

علی مدیر یک پروژه پل‌سازی است که به پایانش نزدیک شده است. در این پروژه ابتدا $n$ پایه بتنی بر روی زمین ساخته شده است، به طوری که پایه‌ی $i$ام در مکان $x_i$ قرار دارد. برای تکمیل پروژه باید مسیر بین پایه‌ی اول ($x_1$) و پایه‌ی آخر ($x_n$) با تعدادی تخته‌‌چوبی به طول $T$ به هم متصل شوند. طبق قوانین پل‌سازی، زیر هر تخته‌چوب باید حداقل $k$ پایه‌ی بتنی وجود داشته باشد، تا تخته‌چوب، سفت در جای خود قرار بگیرد. علی می‌خواهد بداند به ازای تمام $k$های بین $1$ و $n$ در صورتی که می‌توان پل را ساخت، به حداقل چند تخته‌چوب نیاز دارد.

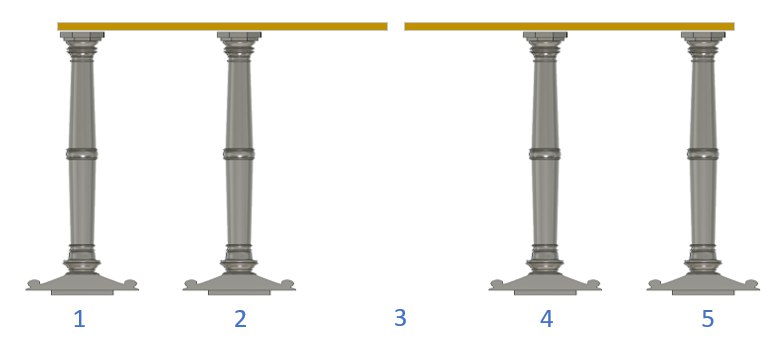
در تصویر بالا جواب مسئله برای $k=2$ برای تست اول نشان داده شده است.

توجه کنید عرض ستون‌ها را صفر در نظر می‌گیریم. فرض کنید یک تخته‌چوب یک بازه‌ی بسته مثل $[x, x + T]$ را متصل می‌کند و ستون‌های شامل این بازه، زیر آن در نظر گرفته می‌شود. شما باید بازه‌ی $[x_1, x_n]$ را متصل کنید و ممکن است تخته چوب‌ها اشتراک داشته باشند.

ورودی

در خط اول ورودی دو عدد طبیعی $n$ و $T$ با فاصله از هم آمده‌ است.

$$1 \le n \le 100 , 000$$ $$1 \le T \le 10^9$$

در خط دوم ورودی $n$ عدد آمده است که مکان پایه‌های بتنی پل را نشان می‌دهد. عدد $i$ام آن برابر $x_i$ است. $$0 \le x_i \le 10^9$$

تضمین می‌شود که $x_1 \lt x_2 \lt \dots \lt x_n,$ باشد.

خروجی

در تنها خط خروجی، $n$ عدد خروجی دهید که نشان‌دهنده‌ی جواب مسئله، به ترتیب به ازای $k$های $1$ تا $n$ باشد و اگر ساختن پل ممکن نبود، به‌جای تعداد تخته‌چوب‌ها -1 چاپ کنید.

ورودی نمونه ۱

4 2
1 2 4 5

خروجی نمونه ۱

2 2 -1 -1 

ورودی نمونه ۲

4 10
0 1 2 20

خروجی نمونه ۲

2 -1 -1 -1