- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۵۱۲ مگابایت
در یک شرکت برنامهنویسی، $n$ برنامهنویس مشغول به کار هستند. این برنامهنویسها با اعداد ۱ تا $n$ شمارهگذاری میشوند. سیستم مدیریتی این شرکت به صورت یک درخت است. یعنی هر برنامهنویس به جز برنامهنویس شمارهی ۱، یک مدیر دارد. مدیر برنامهنویس $i$ را با $p_i$ نشان میدهیم. در واقع ساختار این شرکت به صورت یک درخت ریشهدار است.
عید نوروز نزدیک است و این برنامهنویسها میخواهند از شرکت خارج شوند و برای سفر به شهر کدکاپ بروند. زمانی برنامهنویس شمارهی $i$ میتواند از شرکت خارج شود که $p_i$ هم از سازمان خارج شده باشد.
برای هر $k$ از ۱ تا $n$ حساب کنید چند زیرمجموعه $k$ عضوی از برنامهنویسها میتوانند از شرکت خارج شوند. چون ممکن است پاسخ خیلی بزرگ باشد، باقیماندهی آن را بر $10^9 + 7$ چاپ کنید.
ورودی
در سطر اول ورودی، عدد صحیح و مثبت $n$ آمده که تعداد برنامهنویسهای شرکت را نشان میدهد. $$2 \leq n \leq 10 , 000$$
در سطر دوم ورودی، $n - 1$ عدد صحیح $p_2, p_3, \dots, p_n,$ میآید. $$1 \leq p_i \lt i$$
خروجی
خروجی $n$ سطر دارد و در سطر $k$ام تعداد حالتهایی که $k$ نفر شرکت را ترک کنند محاسبه کنید.
مثالها
ورودی نمونه ۱
3
1 1
خروجی نمونه ۱
1 2 1
توضیح نمونه ۱
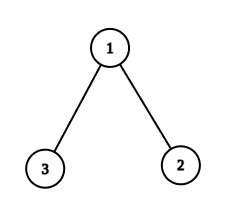
- برای حالت $k = 1$ فقط باید یک برنامهنویس شرکت را ترک کند و آن فقط $1$ است. (۱ حالت)
- برای حالت $k = 2$ فقط باید دو برنامهنویس شرکت را ترک کنند و آنها میتوانند $1, 2$ یا $1, 3$ باشند. (۲ حالت)
- برای حالت $k = 3$ فقط باید سه برنامهنویس شرکت را ترک کنند و آنها میتوانند $1, 2, 3$ هستند. (۱ حالت)
ورودی نمونه ۲
5
1 1 2 2
خروجی نمونه ۲
1 2 3 3 1
توضیح نمونه ۲
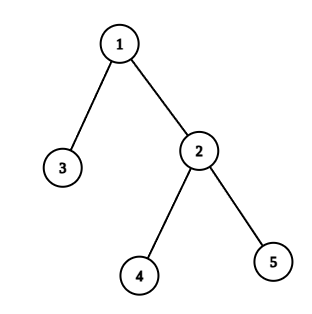
مشابه نمونهی قبل مجموعه افرادی که میتوانند خارج شوند عبارت است از:
$$k = 1 \to {1}$$ $$k = 2 \to {1, 2}, {1, 3}$$ $$k = 3 \to {1, 2, 3}, {1, 2, 4}, {1, 2, 5}$$ $$k = 4 \to {1, 2, 3, 4}, {1, 2, 3, 5}, {1, 2, 4, 5}$$ $$k = 5 \to {1, 2, 3, 4, 5}$$
ارسال پاسخ برای این سؤال