سلام دوست عزیز😃👋
به مسابقه «**کدکاپ ۸ - انتخابی ۲**» خوش آمدی!
لینکهای مفید برای شرکت در مسابقه:
+ [قالب صورت سؤال](/course/assignments/2693/problems/8773)
+ [نحوهی کار با ورودی و خروجی](/course/assignments/2693/problems/8774)
+ [قوانین شرکت در مسابقات](/course/assignments/2693/problems/33523)
+ [انواع خطا در سیستم داوری](https://quera.org/course/assignments/2693/problems/8776)
میتوانید سوالها و مشکلات خود را از بخش «[سوال بپرسید](https://quera.org/contest/clarification/64033/)» با ما در میان بگذارید.
**هرگونه استفاده از ابزارهای آمادهی تولید کد مثل chatGPT و یا تبادل کد با سایر شرکتکنندگان مسابقه ممنوع است و منجر به حذف شما از رقابت میشود.**
**این مسابقه آخرین مسابقهی سال ۱۴۰۲ است و به نام آن عبارت «خداحافظ ۱۴۰۲» اضافه میشود.**
موفق باشید و بهتون خوش بگذره 😉✌
+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۵۱۲ مگابایت
----------
در یک شرکت برنامهنویسی، $n$ برنامهنویس مشغول به کار هستند. این برنامهنویسها با اعداد ۱ تا $n$ شمارهگذاری میشوند. سیستم مدیریتی این شرکت به صورت یک درخت است. یعنی هر برنامهنویس به جز برنامهنویس شمارهی ۱، یک مدیر دارد. مدیر برنامهنویس $i$ را با $p_i$ نشان میدهیم. در واقع ساختار این شرکت به صورت یک درخت ریشهدار است.
عید نوروز نزدیک است و این برنامهنویسها میخواهند از شرکت خارج شوند و برای سفر به شهر کدکاپ بروند. زمانی برنامهنویس شمارهی $i$ میتواند از شرکت خارج شود که $p_i$ هم از سازمان خارج شده باشد.
برای هر $k$ از ۱ تا $n$ حساب کنید چند زیرمجموعه $k$ عضوی از برنامهنویسها میتوانند از شرکت خارج شوند. چون ممکن است پاسخ خیلی بزرگ باشد، باقیماندهی آن را بر $10^9 + 7$ چاپ کنید.
# ورودی
در سطر اول ورودی، عدد صحیح و مثبت $n$ آمده که تعداد برنامهنویسهای شرکت را نشان میدهد.
$$2 \leq n \leq 10 \, 000$$
در سطر دوم ورودی، $n - 1$ عدد صحیح $p_2, p_3, \dots, p_n\,$ میآید.
$$1 \leq p_i \lt i$$
# خروجی
خروجی $n$ سطر دارد و در سطر $k$ام تعداد حالتهایی که $k$ نفر شرکت را ترک کنند محاسبه کنید.
# مثالها
## ورودی نمونه ۱
```
3
1 1
```
## خروجی نمونه ۱
```
1 2 1
```
<details>
<summary>
**توضیح نمونه ۱**
</summary>
----------
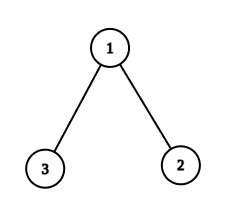
+ برای حالت $k = 1$ فقط باید یک برنامهنویس شرکت را ترک کند و آن فقط $1$ است. (۱ حالت)
+ برای حالت $k = 2$ فقط باید دو برنامهنویس شرکت را ترک کنند و آنها میتوانند $1, 2$ یا $1, 3$ باشند. (۲ حالت)
+ برای حالت $k = 3$ فقط باید سه برنامهنویس شرکت را ترک کنند و آنها میتوانند $1, 2, 3$ هستند. (۱ حالت)
----------
</details>
## ورودی نمونه ۲
```
5
1 1 2 2
```
## خروجی نمونه ۲
```
1 2 3 3 1
```
<details>
<summary>
**توضیح نمونه ۲**
</summary>
----------
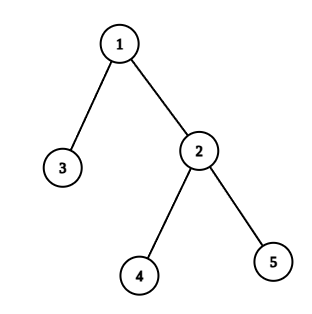
مشابه نمونهی قبل مجموعه افرادی که میتوانند خارج شوند عبارت است از:
$$k = 1 \to \{1\}$$
$$k = 2 \to \{1, 2\}, \{1, 3\}$$
$$k = 3 \to \{1, 2, 3\}, \{1, 2, 4\}, \{1, 2, 5\}$$
$$k = 4 \to \{1, 2, 3, 4\}, \{1, 2, 3, 5\}, \{1, 2, 4, 5\}$$
$$k = 5 \to \{1, 2, 3, 4, 5\}$$
----------
</details>
خروج از سازمان
ارسال پاسخ برای این سؤال
در حال حاضر شما دسترسی ندارید.
