• محدودیت زمان: ۱ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

---

عمو پس از بازنشستگی درکنار مزرعه‌داری به سراغ نقاشی رفت. او یک کاغذ که به مربع های واحد تقسیم شده بود را برداشت. سپس $n$ مربع از آن را انتخاب کرد. $i$م مربع دارای مختصات $(x_i, y_i)$ بود. سپس هر کدام از آن‌ها را به یکی از دو رنگ آبی و قرمز رنگ کرد به طوری که حتما در هر ستون حداکثر یک قرمز و در هر سطر حداکثر یک آبی باشد.

برای مثال شکل زیر یک رنگ آمیزی ممکن عمو است:

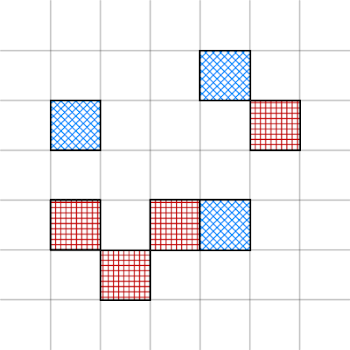
حال عمو می‌خواهد بداند به چند طریق مختلف میتوانسته مربع‌های انتخابی خود را رنگ کند. البته چون جواب ممکن است بزرگ باشد، آن را به پیمانه $10^9 + 7$ خروجی دهید. دو حالت رنگ آمیزی مختلف هستند اگر مربعی باشد که در آن دو حالت دو رنگ مختلف شده باشد

ورودی

در خط اول ورودی شامل عدد $n$ یا همان تعداد مربع‌های انتخاب شده داده می‌شود. در $n$ خط بعدی در هر خط دو عدد داده می‌شود. عدد اول شماره ستون و عدد دوم شماره سطر است.

خروجی

در تنها خط خروجی جواب مسئله را چاپ کنید.

محدودیت‌ها

$$1 \leq n \leq 2 \times 10^5$$ $$-10^9 \leq x_i, y_i \leq 10^9$$

ورودی نمونه ۱

7
-2 2
1 0
-2 0
1 3
2 2
0 0
-1 -1

خروجی نمونه ۱

14

این ورودی همان تصویر داخل متن سوال است.

ورودی نمونه ۲

6
1 1
1 3
5 1
5 3
2 1
2 3

خروجی نمونه ۲

0