محدودیت زمان: ۱ ثانیه
محدودیت حافظه: ۲۵۶ مگابایت

مسئله‌ی قبل را در نظر بگیرید. یک زمین بازی را خوب می‌نامیم که علاوه بر اینکه مستطیل شکل باشد و در آن هیچ موزاییک خرابی وجود نداشته باشد؛ از هیچ یک از اضلاعش قابل گسترش نباشد. این بار از شما می‌خواهیم تعداد زمین‌های خوب را بیابید.

ورودی

در خط اول ورودی، به ترتیب $X$ (اندازه‌ی طول زمین) و $Y$ (اندازه‌ی عرض زمین) با یک فاصله از هم وارد می‌شود.
در خط سوم ورودی، $n$ (تعداد موزاییک های خراب) وارد می‌شود.
سپس در $n$ خط بعدی در هر خط دو عدد طول و عرض مختصات موزاییک‌های شکسته شده با یک فاصله از هم وارد می‌شوند.

توجه: برخلاف سوال قبل، در ورودی این سوال $S$ (تعداد موزاییک‌های زمین انتخابی) نداریم.

$$ 1 \le X, Y \le 250 $$ $$ 0 \le n \le X * Y $$ $$ 1 \le x_i \le X $$$$ 1 \le y_i \le Y $$

خروجی

خروجی تنها شامل یک عدد است که تعداد زمین‌های خوب را نمایش می‌دهد.

مثال

ورودی نمونه ۱

8 2
1
3 1

خروجی نمونه ۱

توضیحات نمونه‌ی ۱

با توجه به تصویر و جدول زیر تعداد زمین‌های خوب ۳ تاست. بنابراین عدد ۳ در خروجی چاپ می‌شود.

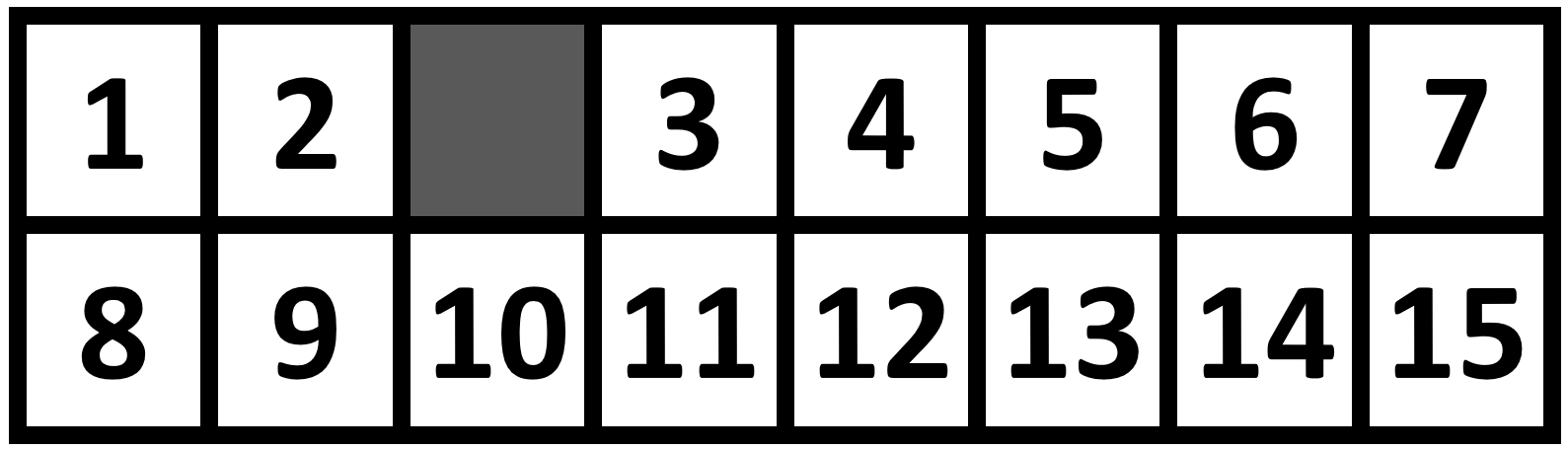
	موزاییک‌های تحت پوشش
زمین خوب ۱	۱ ۲ ۸ ۹
زمین خوب ۲	۳ ۴ ۵ ۶ ۷ ۱۱ ۱۲ ۱۳ ۱۴ ۱۵
زمین خوب ۳	۸ ۹ ۱۰ ۱۱ ۱۲ ۱۳ ۱۴ ۱۵

ورودی نمونه ۲

خروجی نمونه ۲

توضیحات نمونه‌ی ۲

با توجه به تصویر و جدول زیر تعداد زمین‌های خوب ۹ تاست. بنابراین عدد ۹ در خروجی چاپ می‌شود.

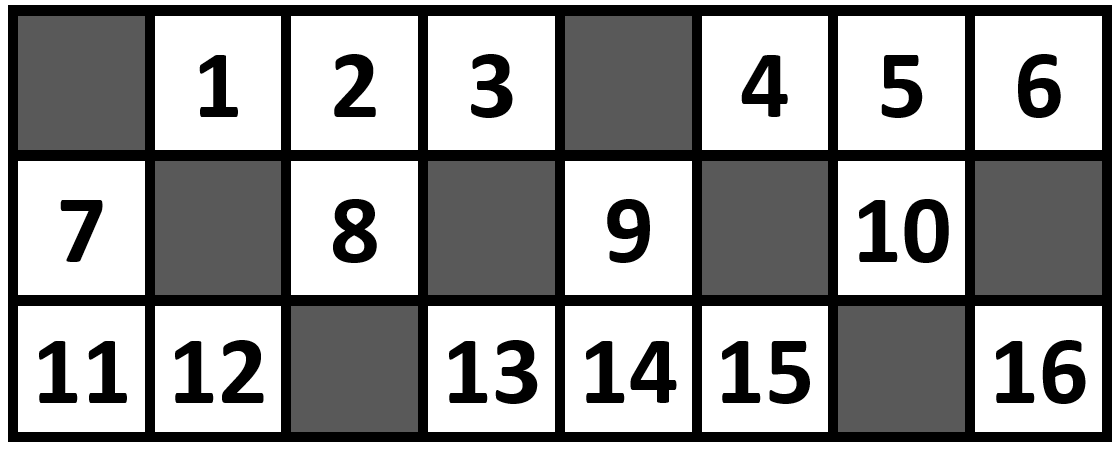
	موزاییک‌های تحت پوشش
زمین خوب ۱	۱ ۲ ۳
زمین خوب ۲	۲ ۸
زمین خوب ۳	۷ ۱۱
زمین خوب ۴	۱۱ ۱۲
زمین خوب ۵	۱۳ ۱۴ ۱۵
زمین خوب ۶	۹ ۱۴
زمین خوب ۷	۴ ۵ ۶
زمین خوب ۸	۵ ۱۰
زمین خوب ۹	۱۶

ارسال پاسخ برای این سؤال