+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- شازززیا دارن یه سری آزمون واسه بچه ها آماده میکنن. ازونجایی خیلی پاش زحمت کشیدن دوس دارن که کلی تبلیغش کنن تا همه بچه ها توش شرکت کنن و میخوان تو شازززلند لوگوی آزموناشونو پخش کنن و برا این کار تصمیم گرفتن از کل ساختمونای خیابون اصلی بعنوان بخشی از لوگو استفاده کنن. لوگو به شکل یه سری راه راه عمودیه با $n$ تا خط که طول هاشون متفاوته و از چپ به راست با $1$ تا $n$ شماره گذاری شده. لوگو با یه جایگشت به شکل $ (s_1, s_2, .... , s_n)$ از اعداد $1$ تا $n$ نمایش داده میشه به طوری که خط شماره ی $s_1$ کوتاه ترین خط باشه بعد از اون بین سایر خط ها خط شماره ی $s_2$ کوتاه ترین باشه و الی آخر تا اینکه خط شماره ی $s_n$ بلند ترین باشه. طول واقعی خط ها اهمیت خاصی نداره. (صرفا اون ترتیبشون مهمه) تو خیابون اصلی شازززلند $m$ تا ساختمون وجود داره که طول هاشون متفاوته. حالا شازززیا که اینو به شکل یه سوال الگوریتمی میدیدن تصمیم گرفتن تعداد بازه هاییو پیدا کنن که لوگو با ساختمون های اون بازه مچ میشه. اما ازون جایی که شازززیا مشغول آماده کردن سوالا هستن نمیتونن خودشون این سوالو حل کنن پس بهشون کمک کنید که تعداد بخش های پیوسته از دنباله ی ساختمون ها رو که با لوگو مچ میشه پیدا کنن. یه دنباله ی پیوسته از ساختمون ها با لوگو مچ میشه اگر ساختمون شماره ی $s_1$ بین دنباله کوتاه ترین باشه و بعد ساختمون شماره ی $s_2$ دومین کوتاه ترین باشه (یعنی بین همه ی ساختمون ها بجز ساختمون شماره ی $s_1$ کوتاه ترین باشه) و الی آخر تا ساختمون شماره $s_n$ که بلندترین باشه. برای مثال یه دنباله از ساختمون ها با ارتفاع های $5,10,4$ با لوگویی مچ میشه که بشکل جایگشت $(3,1,2)$ باشه، از اونجایی که ساختمون شماره ی $3$ با ارتفاع $4$ از همه کوتاه تره و ساختمون شماره ی $1$ دومین کوتاه ترینه و ساختمون شماره ی $2$ بلندترینه. # ورودی در سطر اول ورودی دو عدد $n$ (تعداد خط های لوگو) و $m$ (تعداد ساختمونای خیابون اصلی شازززلند) اومده. $$ 2 \le n \le m \le 10^6 $$ در سطر دوم ورودی جایگشت $s$ که لوگو باهاش نشون داده میشه اومده. (جایگشت از اعداد $1$ تا $n$ می باشد) اگر $ i \neq j $ آنگاه $ s_i \neq s_j $ میباشد. $$ 1 \le s_i \le n $$ در سطر سوم ورودی $m$ تا عدد اومده که $h_i$ ارتفاع ساختمون $i$ ام تو خیابون اصلیه. همه ی $h_i$ ها متفاوتند. $$ 1 \le i \le m $$$$1 \le h_i \le 10^6 $$ # خروجی در تنها سطر خروجی تعداد زیربازه های زیبا رو چاپ کنید. 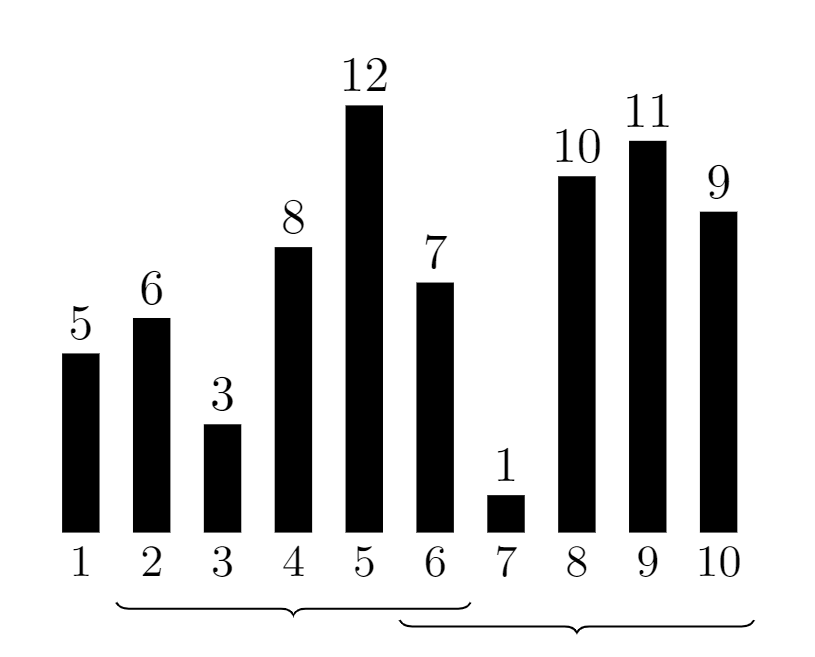# زیرمسئله‌ها | زیرمسئله | نمره | محدودیت |:------------------:|:----------:|:------------------:| | ۱ | ۲۰ | $$ n \le 5000\ ,\ m \le 20000$$ | | ۲ | ۳۰ | $$ n \le 50000\ ,\ m \le 200000$$ | | ۳ | ۳۰ | آرایه $h$ حداکثر $3×10^6$ نا‌به‌جایی دارد | | ۴ | ۲۰ | بدون محدودیت اضافی | # مثال ## ورودی نمونه ۱ ``` 5 10 2 1 5 3 4 5 6 3 8 12 7 1 10 11 9 ``` ## خروجی نمونه ۱ ``` 2 ```  هر دو دنباله ی $6, 3, 8, 12, 7$ و $7, 1, 10, 11, 9$ با لوگوی نشان داده شده با جایگشت $(2, 1, 5, 3, 4)$ مچ میشن.