+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- یک دنباله مثل $a_1, a_2, \dots, a_n \,$ «هندسی‌وار» می‌گوییم اگر برای هر $n \geq 3$ داشته باشیم: $${a_{n - 1}}^2 = a_{n} \times a_{n - 2}$$ همه دنباله‌های به طول ۱ و ۲ «هندسی‌وار» هستند. به یک مستطیل «جذاب‌وار» می‌گوییم اگر هر سطر آن از چپ به راست و هر ستون آن از پایین به بالا یک دنباله «هندسی‌وار» باشد. یک جدول $n \times m$ داریم می‌خواهیم بزرگ‌ترین زیر مستطیلی از آن را پیدا کنیم که «جذاب‌وار» باشد. # ورودی در سطر اول ورودی عدد صحیح و مثبت $n$ و $m$ که با یک فاصله از هم جداشده‌اند آمده. $$1 \leq n, m \leq 1000$$ در $n$ سطر بعدی در هر سطر $m$ عدد صحیح و مثبت که با یک فاصله از هم جداشده آمده است. $$1 \leq a_{i, j} \leq 10^9$$ # خروجی در تنها سطر خروجی مساحت بزرگ‌ترین زیرمستطیل «جذاب‌وار» را چاپ کنید. 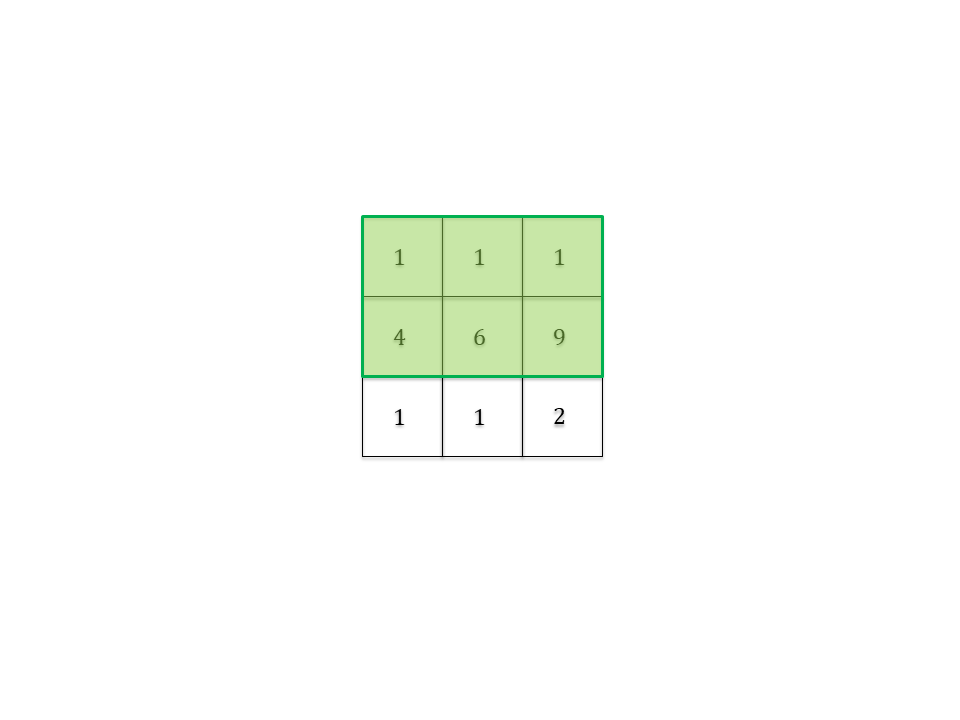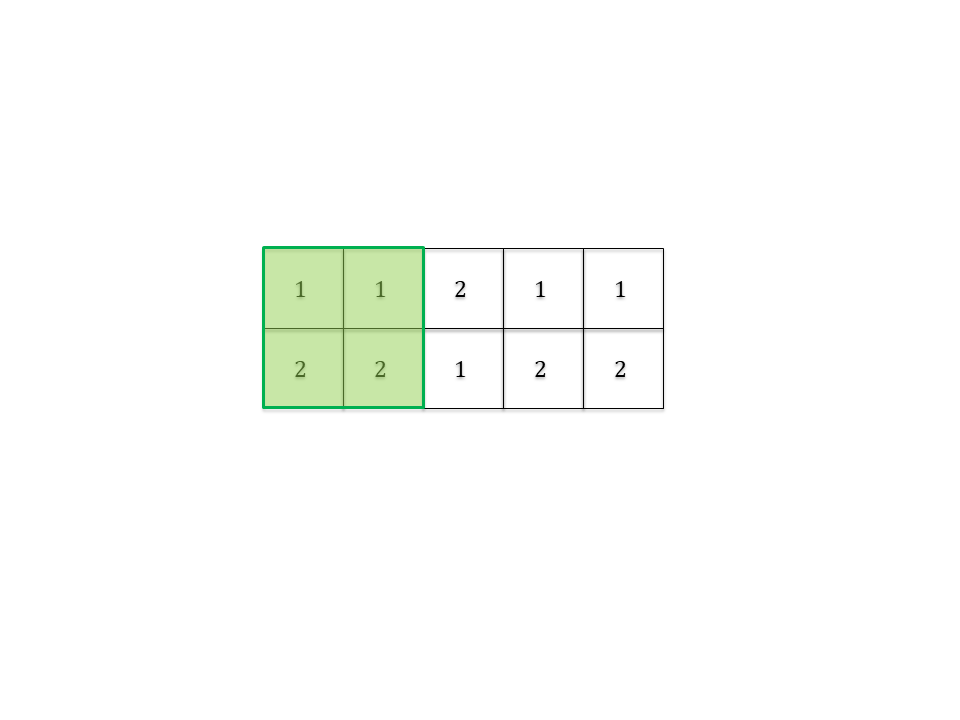# مثال‌ها ---------- ## ورودی نمونه ۱ ``` 3 3 1 1 1 4 6 9 1 1 2 ``` ## خروجی نمونه ۱ ``` 6 ``` <details class="white"> <summary>**توضیح نمونه ۱**</summary>  </details> ---------- ## ورودی نمونه ۲ ``` 2 5 1 1 2 1 1 2 2 1 2 2 ``` ## خروجی نمونه ۲ ``` 4 ``` <details class="white"> <summary>**توضیح نمونه ۲**</summary>  </details>

حل سؤال در بانک سؤالات