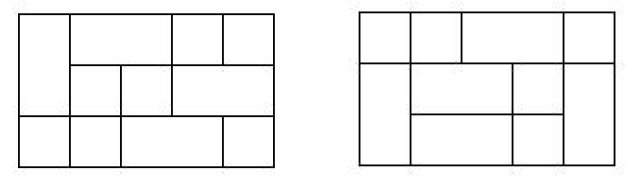
---------- André Claude Marzipan is the head chef at the French restaurant Le Chaud Chien. He owns a vast number of baking trays, which come in two sizes: $1$ foot by $1$ foot, and $1$ foot by $2$ feet. He stores them along $3$-foot deep shelves of various lengths. For example, on a shelf that is $5$ feet long, he might store baking trays in either of the two ways shown below:  Of course, there are many more than just these two ways, and in his off hours André often wonders how many different ways he can place trays on a given shelf. André is a bit of un maniaque du rangement (neat freak), so he insists that the trays are always aligned along the two axes defined by the shelf edges, that the edges of the trays are always $1$ foot multiples away from any edge, and that no portion of a tray extends beyond the shelf. The matter is complicated by the fact that often there are locations on the shelf where he does not want to put any baking trays, due to leaks above the shelf, dents in the shelf’s surface, etc. Since André is more adept at cuisine than counting, he needs a little help. # Input The input consists of two lines: the first line will contain two integers $m, n$, where $1 \le m \le 24$ indicates the length of the shelf (which is always $3$-feet deep) and $n$ indicates the number of bad locations on the shelf. The next line will contain $n$ coordinate pairs $x y$ indicating the locations where trays should not be placed, where $0 < x < m$ and $0 < y < 3$. No location will have integer coordinates and coordinates are specified to the nearest hundredth. If $n = 0$, this second line will be blank. # Output Output the number of ways that trays could be placed on the shelf. ## Sample Input 1 ``` 4 0 ``` ## Sample Output 1 ``` 823 ``` ## Sample Input 2 ``` 4 2 0.29 2.44 2.73 1.8 ``` ## Sample Output 2 ``` 149 ``` ---------------------------------- <details class="blue"> <summary> راهنمایی ۱ </summary> ابتدا فرض کنید مکان بد نداریم و سینی‌ها را در همه‌جای جدول $3 * m$ (همان تاقچه‌ی گفته شده در مسئله)‌ می‌توان قرار داد. حال فرض کنید می‌خواهیم از چپ به راست حرکت کنیم و با استفاده از برنامه‌نویسی پویا، مقدار فعلی مورد نظر را از مقادیر قبلی به دست آوریم. بدین منظور $dp[i]$ را تعریف می‌کنیم، تعداد روش‌های گذاشتن سینی‌ها در یک جدول $3 * i$. با اندکی تفکر در می‌یابیم که رابطه‌ی بازگشتی که این $dp$ را اپدیت می‌کند،‌ خیلی سخت و طولانی است و بنابراین می‌توان نتیجه گرفت که راه مناسبی برای حل مسئله نیست. پس چه کنیم ؟!!! برای اینکه $dp$ ما از مقادیر قبلی قابل اپدیت شدن باشد،‌ میاییم به آن یک بعد اضافه می‌کنیم که بعد جدید نشان‌دهنده‌ی وضعیت دو ستون آخر می‌باشد که آیا ۶ خانه‌ی این دو ستون تاکنون پر شده‌اند یا نه. حال می‌توانیم با گذاشتن یک دومینو به وضعیت جدیدی برویم و مقدار آن وضعیت جدید را از مقدار خود اپدیت کنیم. حال کمی تعریف را دقیق کنیم. $dp[i][mask]$ را تعریف می‌کنیم تعداد روش‌های گذاشتن سینی در $i$ ستون اول به طوری که ستون‌های ‍۱ تا $i - 2$ به صورت کامل با سینی پر شده باشند و $mask$ هم نشان‌دهنده‌ی وضعیت دو ستون آخر باشد. توجه داشته باشید که $mask$ عددی از ۰ تا ۶۳ است که اگر آن را به چشم یک عدد ۶ بیتی در مبنای دو نگاه کنیم، بیت‌های آن نشان‌دهنده‌ی وضعیت دو ستون آخر ما هستند. علت اینکه $mask$ را وضعیت دو ستون آخر گرفتیم این بود که ما اکنون می‌خواهیم سینی‌هایی را قرار دهیم که حتما در ستون $i$ ام خانه‌ای را اشغال می‌کنند و به وضوح این سینی‌ها با ستون‌های ۱ تا $i - 2$ اشتراکی ندارند. </details> ---------------------------------- <details class="blue"> <summary> راهنمایی ۲ </summary> اکنون فرض کن خانه‌های بد نیز وجود دارند و ما نمی‌توانیم داخل این خانه‌ها سینی قرار دهیم. تنها تفاوتی که این مسئله با حالت قبل دارد، این است که ما هیچ‌گاه $dp[i][mask]$هایی که در $mask$ وضعیت یک خانه‌ی بد خالی نشان داده‌ می‌شود را اپدیت نمی‌کنیم. در واقع می‌توانیم فرض کنیم که خانه‌های بد از ابتدا پر بوده‌اند و لذا مقدار تعدادی از استیت‌های $dp$ برابر صفر خواهند شد. این تنها تفاوت این قسمت و حالت قبل است. </details>