+ محدودیت زمان: ۲ ثانیه + محدودیت حافظه: ۵۱۲ مگابایت *****  چند روز پیش و مصادف با روز بعد از اعلام نتایج امتحان هندسه‌ی میان‌ترم، کاراکتر کمکی ۱ در انباری خانه‌شان یک صفحه بازی پیدا کرده که متعلق به پدربزرگ مرحومش (خدا رفتگان شما را هم بیامرزد) است. کاراکتر کمکی ۱ با پیداکردن این صفحه‌ی بازی بسیار خوشحال می‌شود و تصمیم می‌گیرد با دوستش کاراکتر کمکی ۲ برای این‌ صفحه‌ی بازی، بازی‌ای ابداع کنند که با انجام آن اندکی از ناراحتی و غم جان‌سوز اعلام نتایج امتحان هندسه فاصله بگیرند. از آنجایی که قبل از این‌که قرار باشد بازی ابداع شود آن‌ها حتما باید نسبت به صفحه‌ی بازی شناخت پیدا کنند. پس به همین منظور راهنمای صفحه‌ی بازی را مطالعه می‌کنند که اطلاعات مندرج در آن به شرح زیر است: + صفحه‌ی بازی شامل $n$ دایره و $n - 1$ پاره خط است که هر سر هر پاره‌خط به یکی از دایره‌ها متصل است. + دایره‌های صفحه با اعداد متمایز ۱ تا $n$ شماره‌گذاری شده‌اند. + دو دایره‌ را در صفحه‌ی بازی همسایه می‌نامیم اگر و فقط اگر یکی از پاره‌خط‌های صفحه‌ باشد که یک سر آن به یکی از این دو دایره و سر دیگرش به دایره‌ی دیگر متصل باشد. + منظور از **حرکت مهره** در این صفحه‌ی بازی، حرکت دادن مهره از دایره‌ای که روی آن قرار دارد به یکی از همسایه‌های خالی از مهره‌ی آن است. + اگر فقط یک مهره بر روی یکی از دایره‌های صفحه داشته باشیم (برخلاف شرایط بازی) تضمین می‌شود می‌توان با چندبار حرکت‌ دادن مهره، آن را به هر یک از دایره‌های دیگر صفحه رساند. بعد از مطالعه‌ی کامل جزئیات دفترچه‌ی راهنما که در بالا آمده بود، کاراکتر کمکی ۱ و کاراکتر کمکی ۲ توانستند یک بازی بسیار مهیج برای این صفحه‌ی بازی ابداع کنند که مشخصات آن به شرح زیر است: + بازی دو نفره است. + هر بازیکن یک مهره‌ی مخصوص به خود دارد. (بازیکن‌ها در حین بازی می‌توانند وضعیت مهره‌ی حریف را ببینند) + هر یک از دو مهره در ابتدا و حین بازی روی یکی از دایره‌های صفحه قرار می‌گیرند. + هیچ‌گاه دو مهره در یک دایره قرار نمی‌گیرند. + با شروع از کاراکتر اصلی ۱، به نوبت هر بازیکن یک‌بار مهره‌ی خود را حرکت می‌دهد. + بازنده‌ی بازی کسی است که نتواند حرکتی انجام بدهد. یعنی دایره‌ی همسا‌یه‌ی خالی‌ای برای او وجود نداشته باشد که بتواند مهره‌اش را به آن حرکت دهد. دارنده‌ی استراتژی برد، کسی است که با هر نوع بازی طرف مقابل، بتواند طوری بازی کند که در انتها، بازی حتما به نفع خودش تمام شود. برنامه‌ای بنویسید که دارنده‌ی استراتژی برد در بازی را مشخص کند. # ورودی در خط اول ورودی عدد طبیعی $n$ داده می‌شود که نشان دهنده تعداد دایره‌های صفحه‌ی بازی است. در $n -1 $ خط بعدی در هر خط شماره‌ی دو دایره آمده‌اند که نشان‌دهنده‌ی وصل‌بودن این دو دایره توسط یکی از پاره‌خط‌های صفحه است. در خط آخر دو عدد طبیعی $x$ و $y$ داده می‌شود که به ترتیب نشان‌دهنده‌ی شماره دایره‌ی محل ابتدایی مهره‌ی کاراکتر کمکی ۱ و کاراکتر کمکی ۲ است. $$2 \leq n \leq 100 \ 000$$ # خروجی در تنها خط خروجی اگر کاراکتر کمکی ۱ دارنده‌ی استراتژی برد است، `karakter e komaki_1` را چاپ کنید و اگر کاراکتر کمکی ۲ دارنده‌ی استراتژی برد است، `karakter e komaki_2` را چاپ کنید. # مثال ## ورودی نمونه ۱ ``` 3 1 2 1 3 1 2 ``` ## خروجی نمونه ۱ ``` karakter e komaki_2 ``` ## ورودی نمونه ۲ ``` 4 1 2 1 3 1 4 3 1 ``` ## خروجی نمونه ۲ ``` karakter e komaki_2 ``` ## ورودی نمونه ۳ ``` 7 1 2 1 6 2 3 2 4 2 5 6 7 3 7 ``` ## خروجی نمونه ۳ ``` karakter e komaki_1 ``` # توضیح در مثال اول مهره‌های کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایره‌های ۱ و ۲ قرار دارند. در حرکت اول کاراکتر کمکی ۱ تنها می‌تواند به دایره‌‌ی ۳ برود. در حرکت بعدی کاراکتر کمکی ۲ نیز تنها یک حرکت دارد و می‌تواند به دایره‌ی شماره‌ی ۱ برود. حرکت بعدی نوبت کاراکتر کمکی ۱ است که هیچ دایره‌ی همسایه‌ی خالی ندارد، پس برنده‌ی بازی کاراکتر کمکی ۲ است.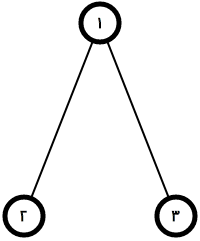 در مثال دوم مهره‌های کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایره‌های ۳ و ۱ قرار دارند. در حرکت اول کاراکتر کمکی ۱ هیچ حرکتی نمی‌تواند انجام بدهد و در همین حرکت اول و بدون هیچ حرکت مهره‌ای کاراکتر کمکی ۲ برنده‌ی بازی است.  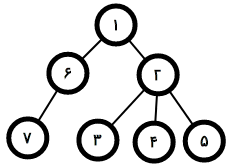در مثال سوم مهره‌های کاراکتر کمکی ۱ و کاراکتر کمکی ۲ به ترتیب در دایره‌های ۳ و ۷ قرار دارند. در حرکت اول کاراکتر کمکی ۱ مجبور است مهره‌اش را به دایره‌ی ۲ ببرد. در حرکت بعدی کاراکتر کمکی ۲ هم مجبور است مهره‌اش را به دایره‌ی ۶ ببرد. از این‌جا به بعد که برای هر یک از دو بازیکن چند حرکت ممکن وجود دارد، برای کاراکتر کمکی ۱ روش برد ارائه می‌دهیم. کاراکتر کمکی ۱ می‌تواند مهره‌اش را به دایره‌ی ۱ ببرد تا کاراکتر کمکی ۲ را مجبور کند در مرحله‌ی بعد مهره‌اش را به دایره‌ی ۷ ببرد و در حرکت آخر کاراکتر کمکی ۱ مهره‌اش را به دایره‌ی ۶ می‌برد تا کاراکتر کمکی ۲ حرکت ممکنی در نوبتش نداشته باشد و برنده‌ی بازی کاراکتر کمکی ۱ شود.