+ محدودیت زمان: ۱ ثانیه + محدودیت حافظه: ۲۵۶ مگابایت ---------- مارچلو در انتهای سفر خود، راه برگشت را گم می‌کند و وارد جنگلی عجیب می‌شود! درختان آن جنگل، همگی به شکل یک [درخت جستجوی دودویی](https://fa.wikipedia.org/wiki/%D8%AF%D8%B1%D8%AE%D8%AA_%D8%AC%D8%B3%D8%AA%D8%AC%D9%88%DB%8C_%D8%AF%D9%88%D8%AF%D9%88%DB%8C%DB%8C) $n$ رأسی بودند که رئوس آن با ۱ تا $n$ شماره‌گذاری شده بودند! مارچلو که با دقت بیشتری به درخت‌های آن جنگل نگاه کرد، متوجه شد که برخی از رأس‌های آنها رنگی هستند. ویژگی این رأس‌ها این است که اگر یک درخت جستجوی دودویی را از یک رأس رنگی ریشه‌دار کنیم، می‌توان طوری جای بچه‌های رئوس (بچه‌های چپ و راست) را جا‌به‌جا کرد که همچنان یک درخت جستجوی دودویی باقی بماند. 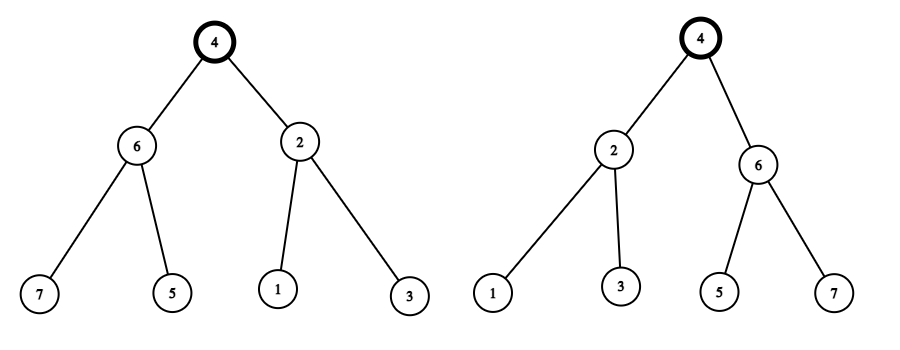(در هنگام جابه‌جایی بچه‌های یک رأس، جای کل زیر درخت‌های آن‌ها با هم عوض می‌شوند) برای مثال با جابه‌جا کردن بچه‌های رأس ۶ و سپس بچه‌های رأس ۴ در درخت دودویی عکس سمت چپ، به درخت جستجوی دودویی در عکس سمت راست خواهیم رسید:  مارچلو که فهمیده بود تمام درخت‌های آن جنگل دقیقاً $k$ رأس رنگی دارند، می‌خواست بداند که حداکثر چند درخت مختلف می‌تواند در آن جنگل وجود داشته باشد. (دو درخت با برچسب‌گذاری یکسان اما ریشه‌ی متفاوت مختلف محسوب می‌شوند) از آنجا که این عدد ممکن است خیلی بزرگ شود، از شما می‌خواهد که باقی‌مانده‌ی تقسیم این عدد بر $10^9 + 7$ را به او بگویید. # ورودی ورودی تنها شامل یک خط است که به ترتیب دو عدد $n$ و $k$ با فاصله از هم آمده است. $$1 \le n, k \le 100\ 000$$ $$k \le n$$ # خروجی در تنها خط خروجی، باقی‌مانده‌ی تقسیم تعداد درخت‌های جستجوی دودویی $n$ رأسی که دقیقاً $k$ رأس رنگی دارند را بر $10^9 + 7$ چاپ کنید. ## ورودی نمونه ۱ ``` 2 1 ``` ## خروجی نمونه ۱ ``` 0 ``` هر درخت جستجوی دودویی دو رأسی دقیقاً دو رأس رنگی دارد، پس جواب برابر صفر خواهد بود. 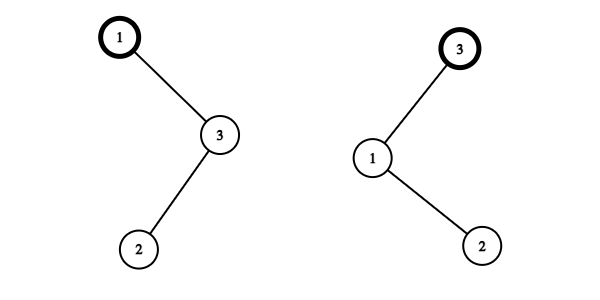## ورودی نمونه ۲ ``` 3 1 ``` ## خروجی نمونه ۲ ``` 2 ``` تنها درخت‌های جستجوی دودویی سه رأسی که دقیقاً یک رأس رنگی دارند در شکل زیر آمده‌اند:  ## ورودی نمونه ۳ ``` 3 2 ``` ## خروجی نمونه ۳ ``` 0 ``` از آنجا که هر درخت جستجوی دودویی سه رأسی یا دقیقاً یک رأس رنگی و یا دقیقاً سه رأس رنگی دارد، پاسخ برابر با صفر خواهد بود.

حل سؤال در بانک سؤالات