+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در کدکاپ سیتی، $n$ خیابان افقی و $m$ خیابان عمودی مانند شکل زیر وجود دارد که هر خیابان افقی و هر خیابان عمودی دقیقاً در یک چهارراه با هم تقاطع دارند. در بالای هر خیابان عمودی یک ماشین به سمت پایین و در پایین آن یک پارکینگ وجود دارد. در سمت راست هر خیابان افقی یک ماشین به سمت چپ و یک پارکینگ در انتهای آن قرار دارد.
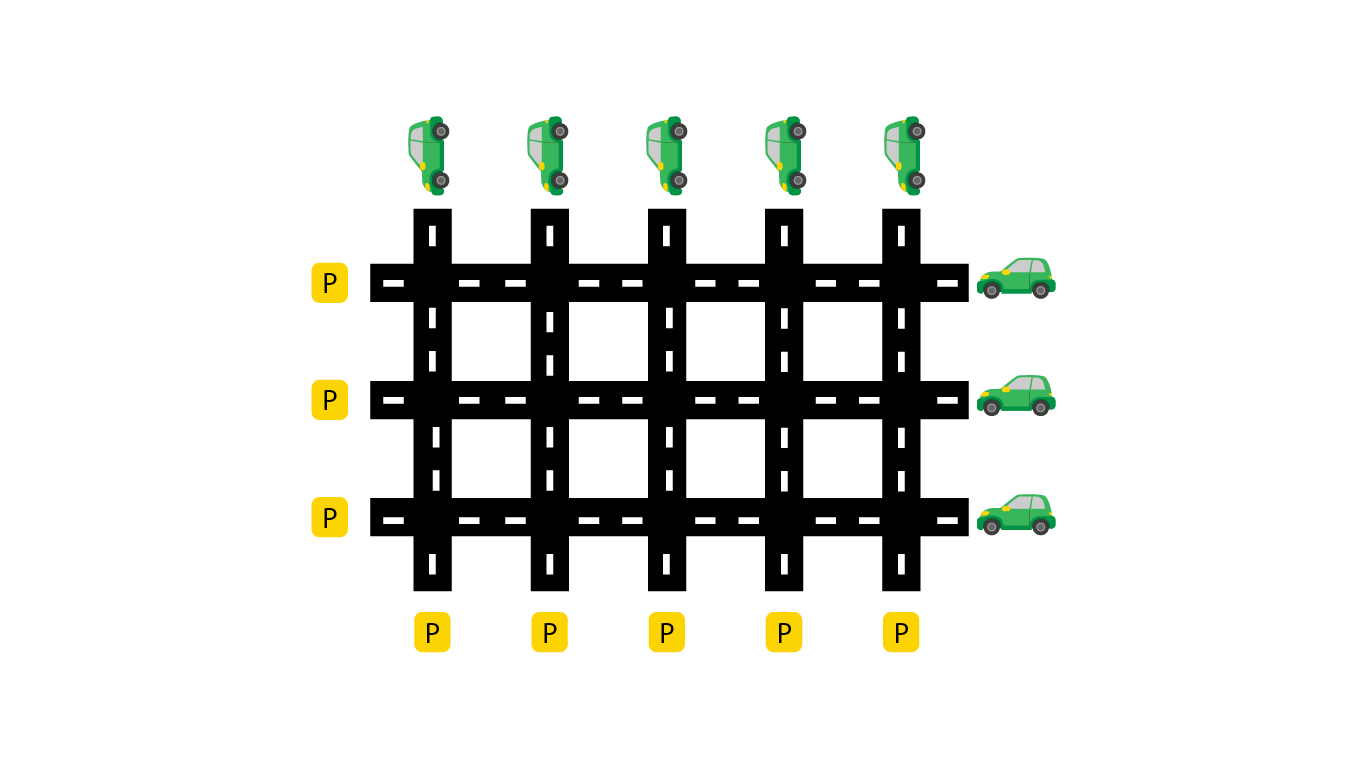
همهی ماشینها در یک لحظه به طور همزمان با سرعت برابر و ثابت شروع به حرکت میکنند. میدانیم عبور از فاصلهی بین دو تقاطع برای یک ماشین، یک دقیقه زمان میبرد. همچنین برای هر ماشین رسیدن به اولین تقاطع نیم دقیقه زمان میبرد و نیم دقیقه زمان میبرد که وارد پارکینگ شود و پارک کند. هرگاه دو ماشین در یک تقاطع به هم برسند یکی از آنها باید یک دقیقه صبر کند تا ماشین دیگر از آن تقاطع عبور کند.
میخواهیم از بین تمام حالتهایی که ممکن است ماشینها در پارکینگ توقف کنند، بررسی کنید کمترین زمانی که لازم است تا همهی ماشینها به پارکینگشان برسند، چقدر است.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد سناریوها را نشان میدهد.
$$1 \leq t \leq 10 \, 000$$
در تنها سطر هر سناریو، دو عدد صحیح $n$، $m$ داده میشود که به ترتیب نشاندهنده تعداد خیابانهای افقی و عمودی است.
$$1 \leq n, m \leq 10^9$$
# خروجی
در $t$ سطر، برای هر سناریو به ترتیب حداقل زمان (بر حسب دقیقه) مورد نیاز برای رسیدن تمام ماشینها به پارکینگشان برسند را در خروجی چاپ کنید.
# مثالها
## ورودی نمونه ۱
```
3
4 4
3 5
1 1
````
## خروجی نمونه ۱
```
5
5
2
````
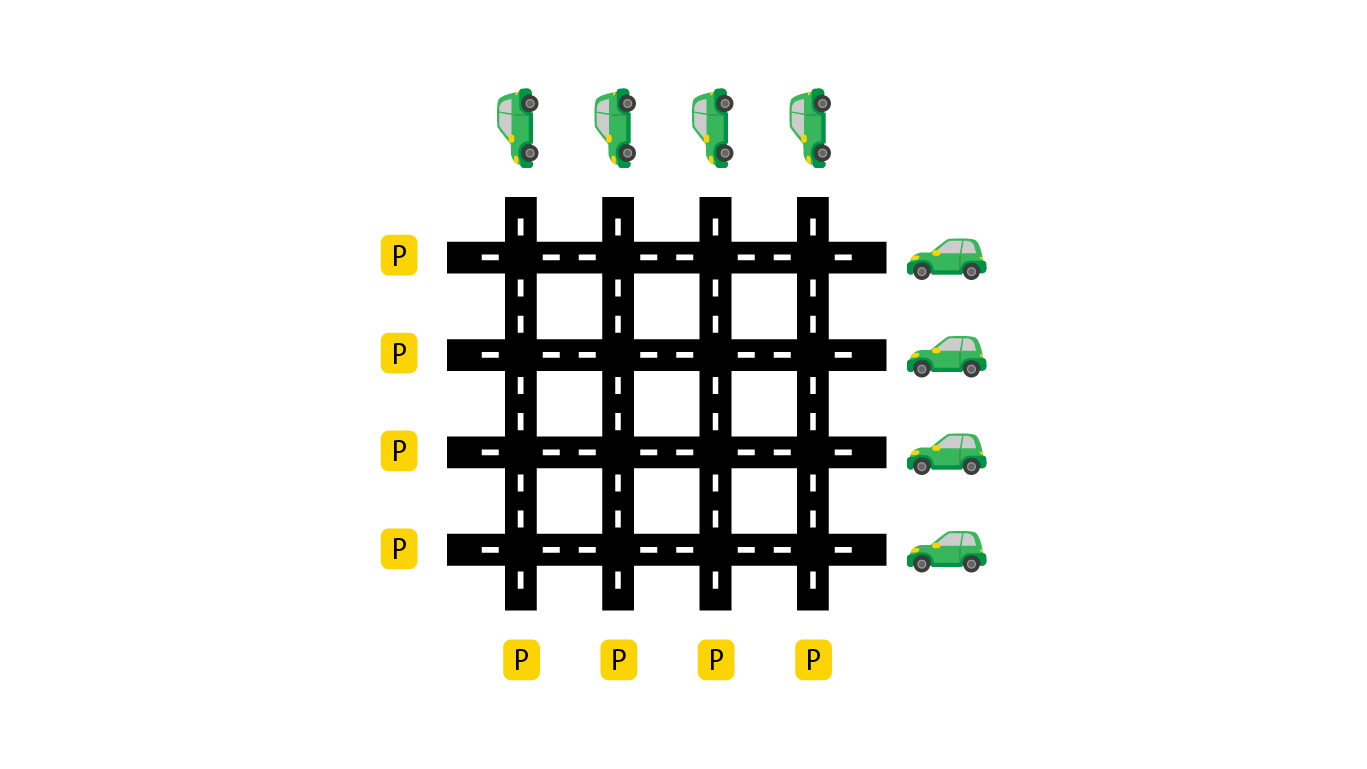
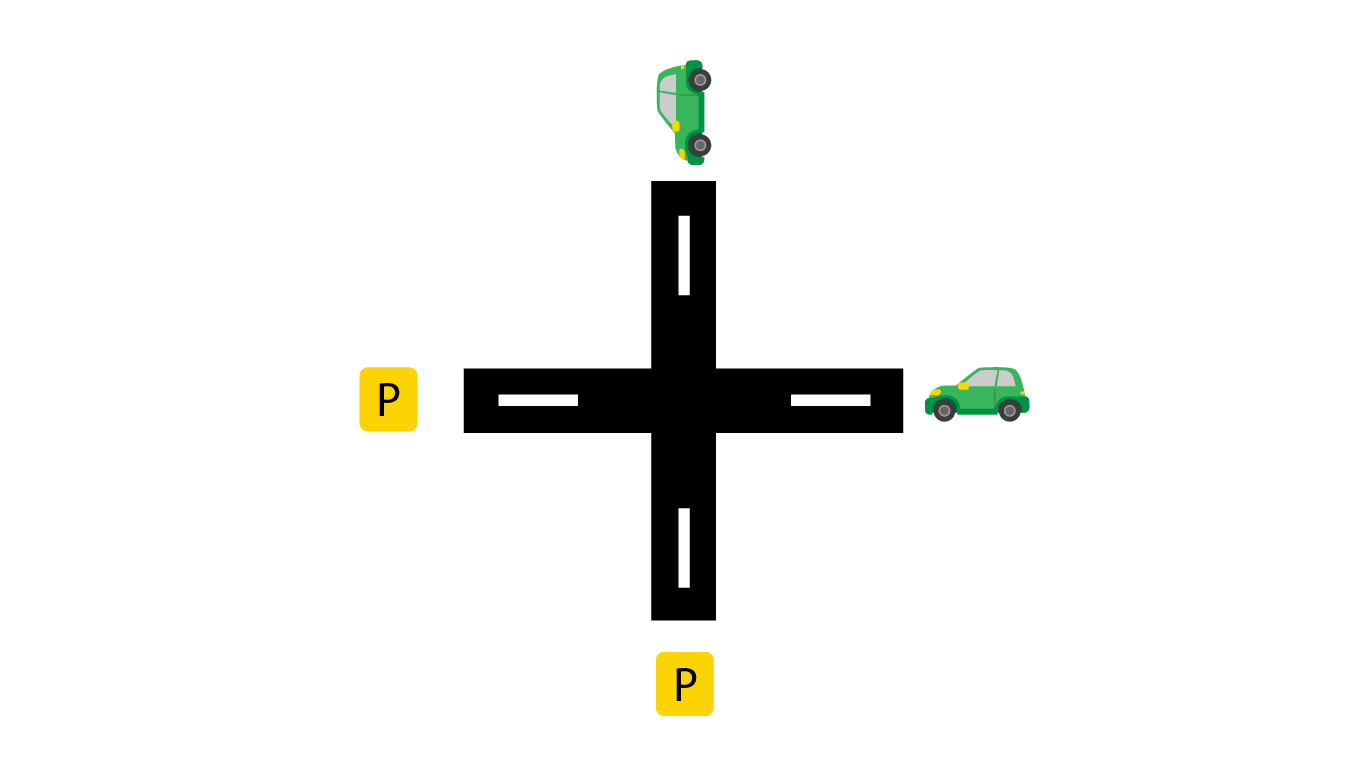
چهارراه کدکاپ
ارسال پاسخ برای این سؤال
در حال حاضر شما دسترسی ندارید.
