+ محدودیت زمان: ۱ ثانیه
+ محدودیت حافظه: ۲۵۶ مگابایت
----------
در مهمانی شام کدکاپ $n$ دانشجوی علوم کامپیوتر، $m$ دانشجوی مهندسی کامپیوتر و $p$ استاد دانشگاه دعوت شدهاند. در سالن پذیرایی $\frac{n + m + p}{4}$ میز دایرهای ۴ نفره قرار داده شده تا هر مهمان روی یک صندلی بنشیند. میدانیم $n + m + p$ به ۴ بخشپذیر است.

از نظر کوئرا دو نفر که دور یک میز دایرهای **کنار هم** نشستهاند، تشکیل یک زوج خوشحال میدهند، اگر:
+ حداقل یکی از این دو نفر استاد دانشگاه باشد.
+ دو دانشجو با رشتههای مختلف باشند.
حالا میخواهیم مهمانها را طوری روی صندلیهای میز بنشانیم که تعداد زوجهای خوشحال، در مجموع، بیشینه شود. از شما میخواهیم برنامهای بنویسید که این مقدار بیشینه را پیدا کند.
# ورودی
در سطر اول ورودی، عدد صحیح $t$ آمده که تعداد سناریوها را نشان میدهد.
$$1 \leq t \leq 10 \,000$$
در تنها سطر هر سناریو، سه عدد صحیح $n$، $m$ و $p$ که به ترتیب نشاندهنده تعداد دانشجویان علوم کامپیوتر، مهندسی کامپیوتر و اساتید است، داده میشود.
$$0 \leq n, m, p \leq 10^9, \quad n + m + p \geq 4$$
تضمین میشود در هر سناریوها، $n + m + p$ مضرب ۴ باشد.
# خروجی
در $t$ سطر، بیشینهی تعداد زوجهای خوشحال را خروجی دهید.
# مثالها
## ورودی نمونه ۱
```
2
8 2 2
4 0 12
````
## خروجی نمونه ۱
```
8
16
````

در این نمونه، اگر $n = 8$ دانشجوی علوم کامپیوتر روی جایگاه زرد، $m = 2$ دانشجوی مهندسی کامپیوتر روی جایگاه بنفش و $p = 2$ استاد دانشگاه روی جایگاههای سبز بنشینند، ۸ زوج خوشحال که با کمانهای قرمز مشخص شده بهوجود میآید و این، بیشینه تعداد ممکن، در بین تمام حالتها است.
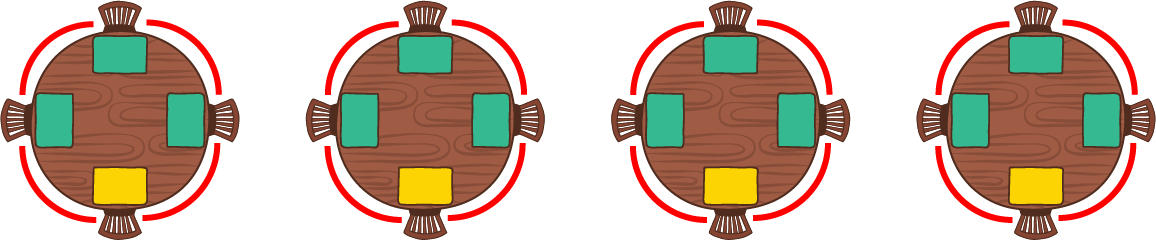
در این نمونه، اگر $n = 4$ دانشجوی علوم کامپیوتر روی جایگاه زرد، و $p = 12$ استاد دانشگاه روی جایگاههای سبز بنشینند، همهی ۱۶ زوج خوشحال میشوند که این، بیشینه تعداد ممکن است.
شام کدکاپ
ارسال پاسخ برای این سؤال
در حال حاضر شما دسترسی ندارید.
