خانه توسعهدهنده تبدیل مبنا؛ چطور مبناها را به یکدیگر تبدیل کنیم؟
تبدیل مبنا؛ چطور مبناها را به یکدیگر تبدیل کنیم؟

۱۲۳؛ همهی ما درک مشترکی از این عدد در زندگی روزمره داریم، اما تا به حال به معنای این عدد توجه کردهاید؟! همهی ما به خوبی میدانیم که اعداد با نمادهای ۰ تا ۹ نمایش داده میشوند. اما به راستی چرا تنها از این ۱۰ نماد استفاده میشود؟ در ابتدای مسیر علوم ریاضی از ۱۰ نماد استفاده میکردند چون اولین ابزار شمارش بشر یعنی دست، دارای ۱۰ انگشت بود! خوب است بدانید به این سیستم شمارش اعداد «هندی-عربی» نیز گفته میشود. با تمام این تفاسیر باید گفت ما همیشه از ۱۰ نماد برای نمایش اعداد استفاده نمیکنیم و از مبناهای متفاوتی برای هر کاربرد استفاده میشود. در این مقاله نحوه «تبدیل مبنا» را بررسی خواهیم کرد.
اگر هنوز مطمئن نیستید که یادگیری برنامهنویسی برایتان مناسب است یا نه، یا نمیدانید از کجا شروع کنید، ما یک کوییز ساده و جذاب آماده کردهایم که میتواند به شما کمک کند مسیر درست را پیدا کنید.
همین حالا امتحان کنید: برنامه نویسی را از کجا شروع کنیم
فهرست مطالب
Toggleمبنا چیست؟
اجازه دهید به دوران ابتدایی برگردیم؛ در کلاس اول برای شمارش از نِی یا چوب استفاده میکردیم و هرگاه تعداد نیها یا چوبها به ۱۰ عدد میرسید، برای نمایش بهتر از یک بسته ۱۰تایی نی استفاده میکردیم و دوباره نیها را تکتک اضافه میکردیم تا به ۱۰ عدد برسند و به جای آنها یک بسته ۱۰تایی دیگر اضافه میکردیم. این دقیقا همان کاری است که برای فهم اعداد استفاده میشود. به مثال زیر دقت کنید:
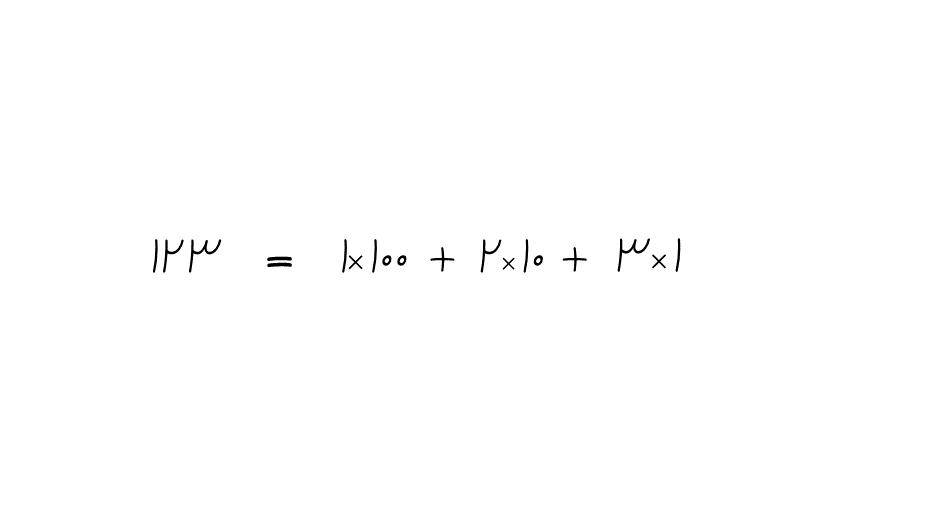
این یعنی عدد ۱۲۳ از ۱ بسته ۱۰۰تایی، ۲ بسته ۱۰تایی و ۳ بسته تکی تشکیل شده است. همانطور که میبینید، برای شمارش از بستههایی استفاده کردهایم که توانی از ۱۰ هستند. در همین مثال بستههای 100، 101 و 102 استفاده شده است. به این سیستم شمارش مبنای ۱۰ یا decimal گفته میشود و یعنی اعداد به صورت وزنهایی (بستههایی) از توان ۱۰ بیان میشوند.
اما آیا همیشه از ۱۰ نماد برای نمایش اعداد استفاده میشود؟! خیر…

اعداد مبنای ۲ (باینری یا دودویی)
با توجه به توضیحات بالا، قابل حدس هست که در مبنای ۲ اعداد در وزنهایی (بسته) از توان ۲ نوشته میشوند و برای همین نیز تنها از ۲ نماد ۰ و ۱ برای نمایش استفاده میگردد. در واقع به دلیل اینکه با هر ۲ شمارش، یک بسته جدید تشکیل میشود نیازی به استفاده از بیش از ۲ نماد وجود ندارد.
به مثال زیر توجه کنید. میخواهیم عدد ۱۱۰ را به عنوان یک عدد باینری (عددی فقط شامل ۰ و ۱) به عدد مبنای ۱۰ تبدیل کنیم. برای این کار باید مانند مثال قبل، عدد را به بستههایی از توان ۲ تبدیل کنیم و مجموع آنها را حساب کنیم.
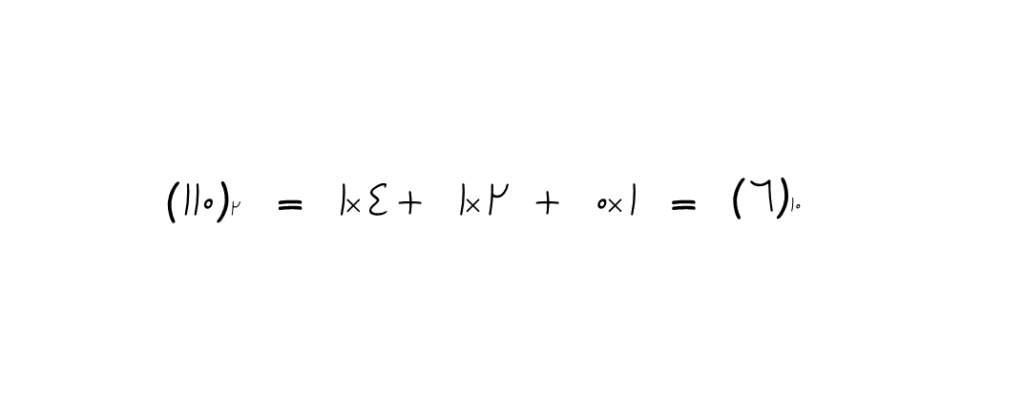
(اعداد نوشته شده در جلوی پرانتز نمایانگر مبنای عدد است)
در اینجا مشابه قبل، عدد ۱۱۰ باینری به معنی این است که ۱ بسته ۴تایی (22)، ۱ بسته ۲تایی (21) و صفر بسته ۱ تایی (20) داریم. بنابرین در مجموع شش نی خواهیم داشت که در مبنای ۱۰ با نماد ۶ نمایش داده میشود.
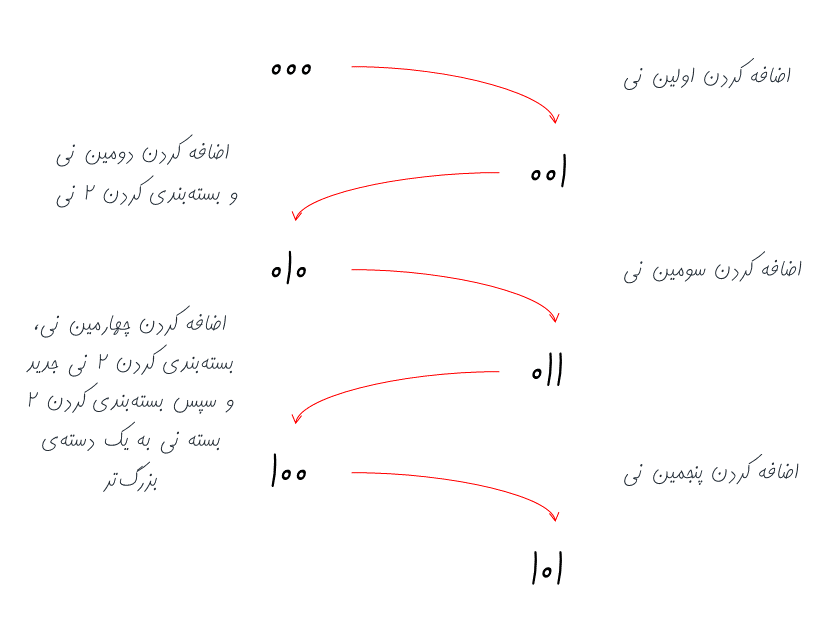
اکنون بیایید عدد ۵ را در مبنای ۲ نمایش دهیم. برای نمایش عدد ۵ شروع به شمردن میکنیم؛ در ابتدا صفر نی داریم (0). یک نی اضافه بر میداریم (1)، با برداشتن یک نی دیگر، میتوان یک بسته ۲تایی تشکیل داد و به جای ۲ نی، یک بسته نی ۲تایی قرار میدهیم (10). ادامه میدهیم و مثل قبل نی اضافه میکنیم تا یک بسته ۲تایی دیگر تشکیل شود. اکنون ۲ بسته نی ۲تایی داریم و میتوان به جای آن، یک بسته نی ۴تایی قرار داد (100). در آخر نیز یک نی دیگر اضافه میکنیم و به عدد ۵ میرسیم (101).
مرحلهبهمرحله اضافهکردن نیها و بستهبندی کردن آنها در بخش زیر آورده شده است:
در پایین میبینید با تبدیل ۱۰۱ از مبنای ۲، به مبنای ۱۰ به عدد ۵ میرسیم.
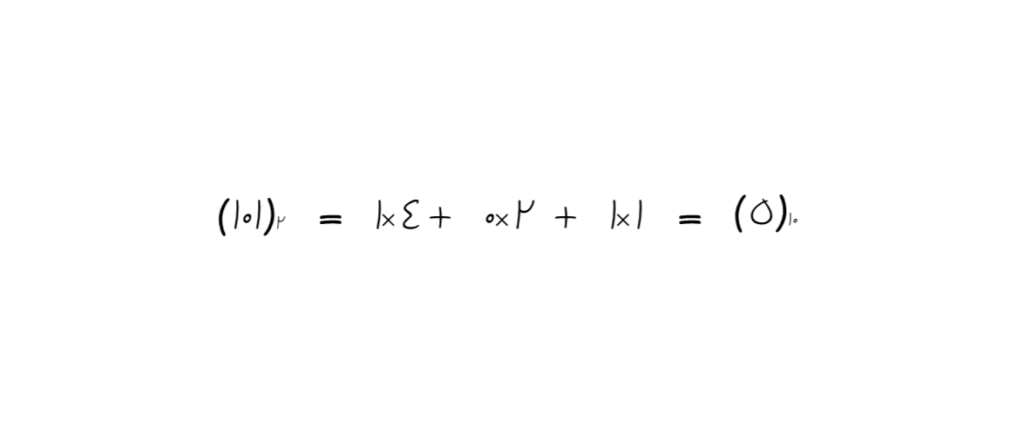
قبل از حرف زدن دربارهی روش تبدیل مبنا، خوب است بدانیم در مبنای ۲، به هر نماد بهکار رفته بیت (bit مخفف binary digit) گفته میشود. یعنی عدد ۱۰۱، ۱۰۰، ۱۱۰، ۱۱۱ همگی ۳ بیت دارند. در دنیای کامپیوتر به هر ۸ بیت یک بایت (Byte) گفته میشود.
به نظر شما، با ۳ بیت تا چه عددی را میتوان شمرد؟ با ۳ بیت میتوان ۸ عدد را شمرد، چون شمارش ما از ۰ شروع میشود، میتوان از ۰ تا ۷ را شمارش نمود. اگر به ریاضیات مراجعه کنیم میتوان دید با ۳ بیت میتوان ۲ به توان ۳ حالت را شمارش کرد.
با n بیت چند عدد را میتوان شمارش نمود؟ همان طور که دیدیم، با n بیت میتوان ۲ به توان n عدد را شمارش کرد که چون شمارش ما از ۰ شروع میشود بازه اعداد از ۰ تا ۲ به توان n منهای ۱ میشود.
بیشتر بخوانید: باینری چیست و چگونه از آن در علوم کامپیوتر استفاده میشود؟
تبدیل مبنای باینری به مبنای ۱۰
برای تبدیل اعداد باینری به مبنای ۱۰، میتوان از همان راهکار بستهها استفاده نمود و هر بیت را در وزن خودش ضرب کرد و حاصل جمع آنها برابر با عدد در مبنای ۱۰ میشود. برای مثال داریم:
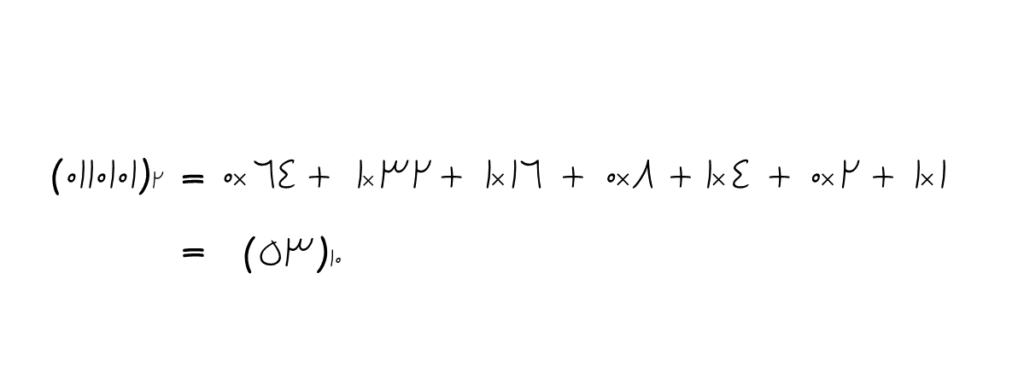
به همین سادگی میتوان اعداد را از مبنای ۲ به مبنای ۱۰ تبدیل کرد. کافی است هر بیت را در وزن خودش (که در اعداد باینری توانی از ۲ است)، ضرب نماییم و سپس همهی آنها را با یکدیگر جمع کنیم.
تبدیل اعداد مبنای ۱۰ به دودویی
تبدیل اعداد مبنای ۱۰ به باینری کمی دشوارتر است. یک روش که قبلتر هم آن را دیدیم، شمارش تکتک است که کاری زمانبر خواهد بود و برای اعداد بزرگ غیرممکن است. روش دیگر که استفاده از آن متداول است، تقسیم متوالی اعداد است. بیایید با این روش بیشتر آشنا شویم.
در روش تقسیم متوالی به این صورت عمل میشود که هربار عدد را بر ۲ تقسیم میکنیم و باقیمانده آن، یک بیت از عدد را تشکیل میدهد. تقسیمها تا زمانی انجام میشوند که به خارج قسمت ۱ برسیم و در پایان، خارج قسمت را به بیتها اضافه میکنیم. به مثال زیر توجه کنید:
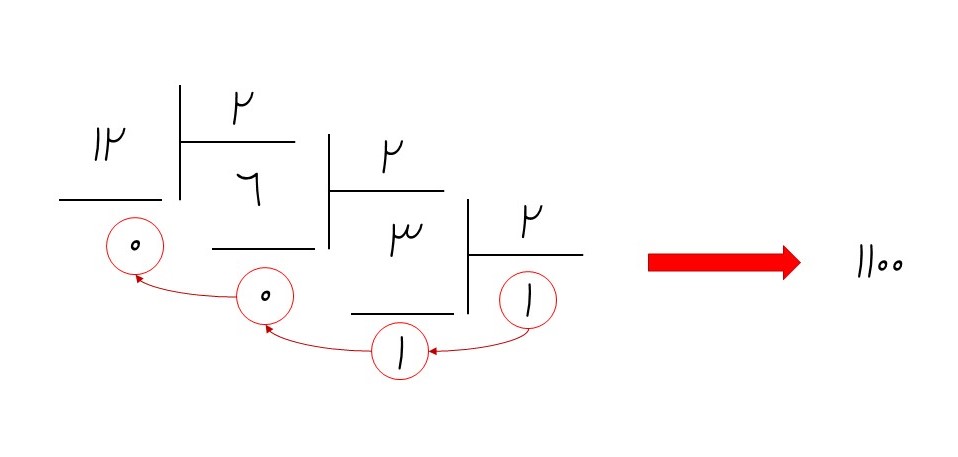
همانطور که میبینید به عدد ۱۱۰۰ باینری رسیدیم و برای اطمینان از روش بهکاررفته، میتوان یک بار عدد را به مبنای ۱۰ تبدیل کرد:
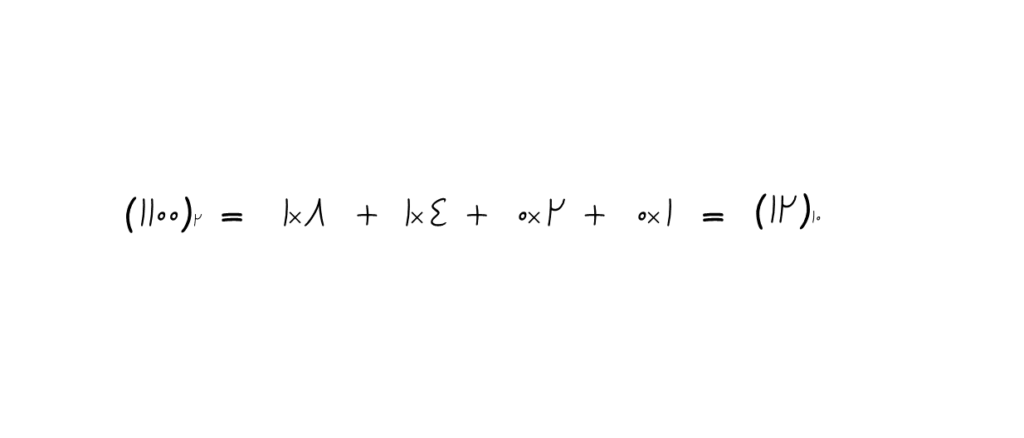
همانطور که انتظار میرفت، با تبدیل به عدد ۱۲ رسیدیم و یعنی روش تقسیم متوالی بهدرستی عدد را از مبنای ۱۰ به مبنای ۲ تبدیل کرده است.
در انتها جدولی از اعداد باینری و معادل مبنای ۱۰ آنها را میبینید. سعی کنید این اعداد باینری را بخاطر بسپارید.
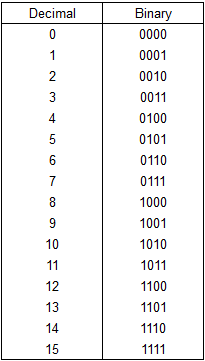
خوب است بدانید در علوم کامپیوتر مبناهای باینری (۲)، اکتال (۸) و هگزادسیمال (۱۶) بیشترین کاربرد را دارند.
تبدیل مبناهای دیگر
میتوان از هر دو روش بالا یعنی تبدیل مبنا از باینری به مبنای ۱۰ یا تبدیل مبنای ۱۰ به باینری، برای تبدیل هر مبنایی به مبنای ۱۰ و برعکس استفاده کرد. کافی است به جای وزنهای توان ۲ از وزنهای توان مبنا و در روش تقسیم متوالی از تقسیم عدد بر مبنا استفاده نمایید.
در مثال زیر قصد داریم یک عدد مبنای ۱۰ را به مبنای ۸ ببریم و یک عدد مبنای ۸ را نیز به مبنای ۱۰ تبدیل کنیم. خوب است قبل از هر چیز، خودتان سعی کنید به جوابها برسید.
توجه کنید که در مبنای ۸، طبق تعریف ۸ نماد وجود دارد (نمادهای ۰ تا ۷)!
عدد ۸(۲۵۴) در مبنای ۱۰ به چه صورتی نمایش داده میشود؟
راهحل
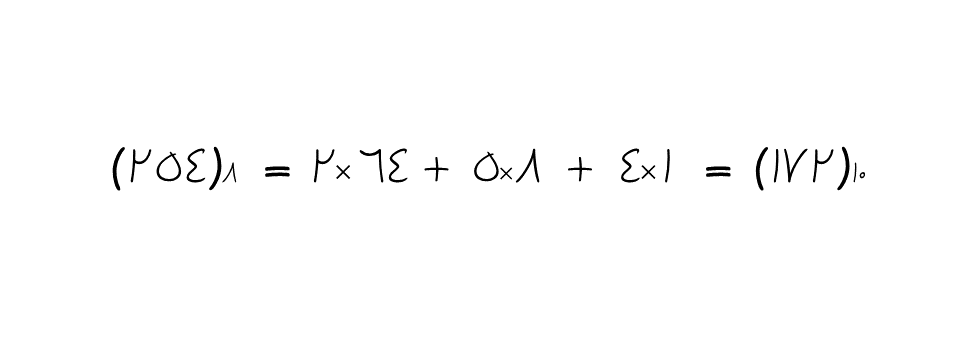
راهحل
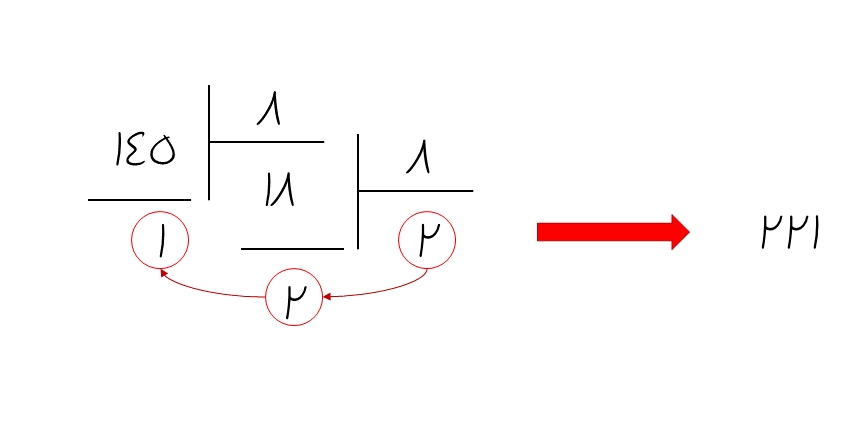
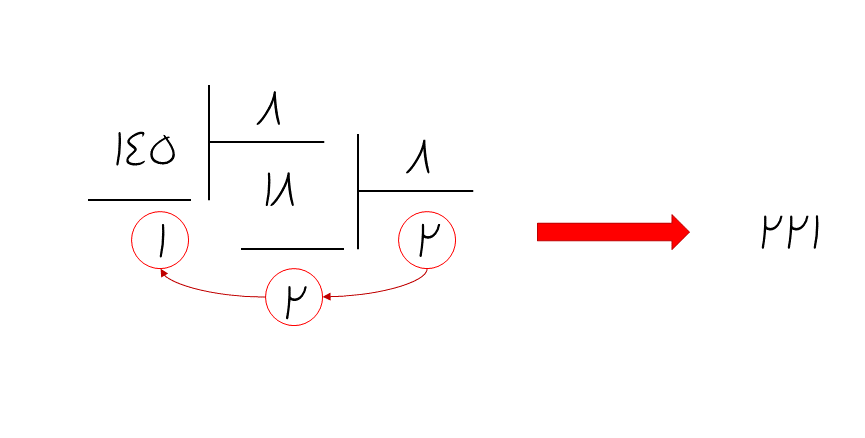
عدد ۱۰(۱۴۵) درمبنای ۸ به چه صورتی نمایش داده میشود؟
راهحل
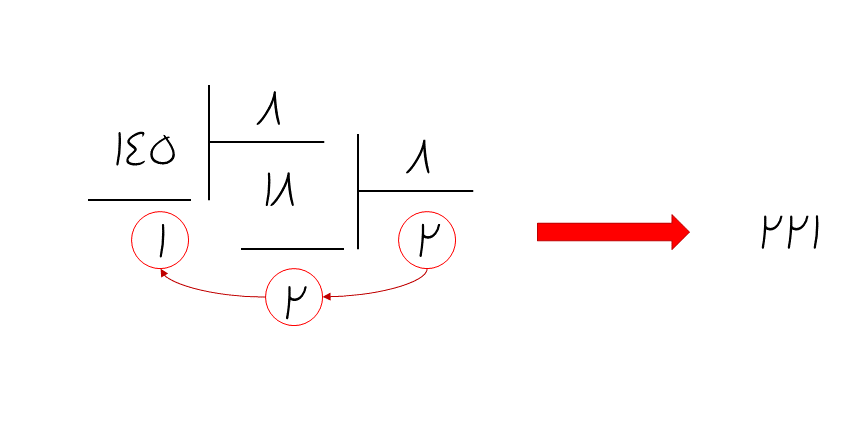
جمعبندی
با توجه به تمامی توضیحات، میتوان دید که اعداد به خودی خود معنایی ندارند و این مبنای اعداد است که به نمادها و ارقام معنا میدهد. در این مقاله با نحوه تبدیل مبناها آشنا شدیم و دیدیم که اعداد در هر مبنایی به راحتی به مبنای ۱۰ که پرکاربردترین مبنا در زندگی روزمرهی ما میباشد، تبدیل میشوند. همینطور توسط الگوریتم تقسیم متوالی میتوان اعداد مبنای ۱۰ را به مبنای دلخواه تبدیل کرد.
در علوم کامپیوتر، همانطور که پیشتر اشاره شد از مبنای ۲ استفاده میشود و در بحثهایی مثل آدرسهای حافظه از مبناهای ۸ و ۱۶ استفاده میشود.
برای کسب اطلاعات بیشتر از اعداد مبنای ۱۰ میتوانید به place value، برای اعداد باینری به binary number system و برای اعداد مبنای ۱۶ به hexadecimals سر بزنید. همچنین برای یادگیری کاربرد مبنا، اعداد باینری و مبانی برنامهنویسی، میتوانید به کالج برنامهنویسی پایتون مقدماتی مراجعه کنید. ممنون از اینکه تا انتهای این مقاله با ما همراه بودید. در نظرات به ما بگویید که مطالعهی این مقاله چقدر برای شما مفید بود.

دانشجوی کارشناسی ارشد هوش مصنوعی، علاقهمند به دنیای دادهها و یادگیری عمیق، مشتاق یادگیری















