الگوریتم ژنتیک در پایتون چیست و چطور پیاده‌سازی می‌شود؟

مدل‌های بهینه‌سازی (Optimization Models) یکی از بهترین ابزارهای در دسترس محققان داده یا دیتا ساینتیست‌ها است که از آن‌ها برای حل مسائل گوناگون استفاده می‌شود، از مسائل مربوط به بهره‌وری گرفته تا پیدا کردن بهینه‌ترین هایپر پارامتر در یک مدل. در این مقاله قصد داریم به سراغ یکی از شناخته‌شده‌ترین مدل‌های بهینه‌سازی برویم: الگوریتم‌های ژنتیک.

از اسم «الگوریتم ژنتیک» احتمالا می‌توانید حدس بزنید که این الگوریتم چطور کار می‌کند. بله، الگوریتم‌های ژنتیک بر پایه‌ی ایده‌های انتخاب طبیعی و ژنتیک ساخته شده‌اند. این الگوریتم‌ها معمولا برای پیدا کردن راه‌حل‌های باکیفیت در مسائل بهینه‌سازی و جستجو استفاده می‌شوند.

با کوئرا بلاگ همراه باشید تا بگوییم الگوریتم ژنتیک چیست و سپس نحوه پیاده‌سازی الگوریتم ژنتیک در پایتون را به صورت قدم‌به‌قدم یاد بگیریم.

اگر نیاز به آشنایی اولیه با زبان پایتون و کسب مهارت‌های درآمدزا دارید، پیشنهاد می‌کنیم با شرکت در دوره آموزش پایتون کوئرا کالج، تسلطی کامل بر این زبان محبوب پیدا کنید.

الگوریتم‌های ژنتیک و مدل‌های بهینه‌سازی

الگوریتم ژنتیک نوعی الگوریتم جمعیتی (Population-Based) و تصادفی (Stochastic) است. اما این دقیقا یعنی چه؟ زمانی که راجع به مدل‌های بهینه‌سازی صحبت می‌کنیم، می‌توانیم آن‌ها را از لحاظ نحوه پیاده‌سازی جستجو در دسته‌بندی‌های زیر قرار دهیم:

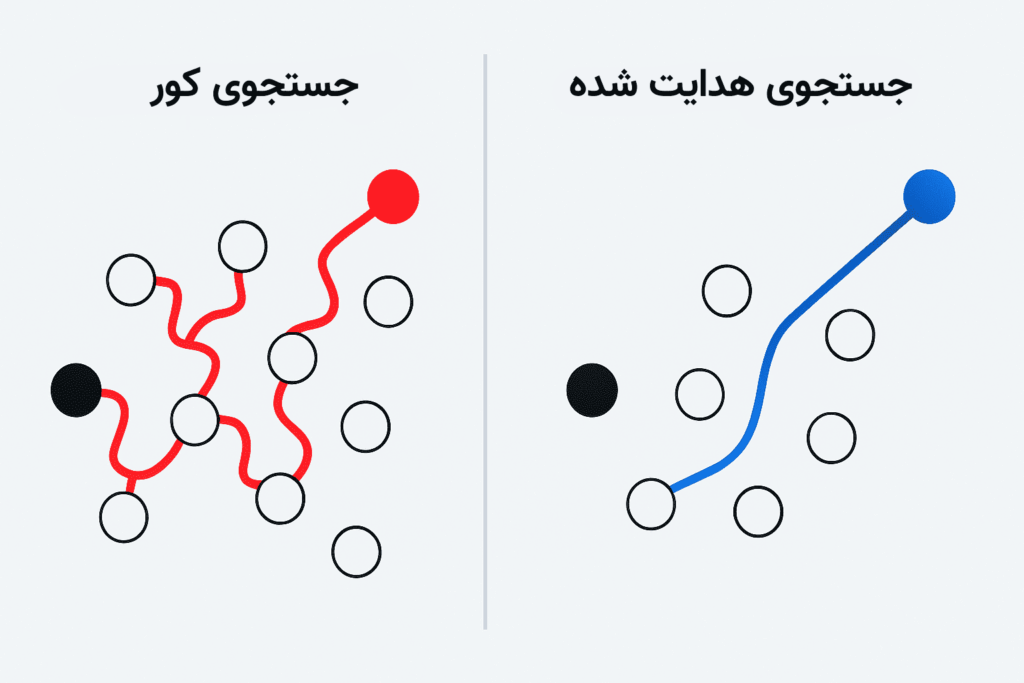
• جستجوی کور (Blind Search): در این رویه، تمام گزینه‌های احتمالی به شکلی گسترده جستجو می‌شوند و مهم نیست که پیش از این چه نتایجی به دست آورده‌ایم.
• جستجوی هدایت‌شده (Guided Search): در این تکنیک، از نتایج قبلی برای هدایت مدل به جستجو نتایج مشابه استفاده می‌شود و به صورت کلی دو نوع جستجو هدایت‌شده داریم:
  • جستجوی تک‌حالت (Single State Search): از مقادیری مشابه به راهکار نخست برای پیدا کردن نتایج استفاده می‌کند. در صورتی که اندکی پیچیدگی در کار باشد، این تابع شکلی همگرا پیدا می‌کند.
  • جستجوی جمعیتی (Population-Based Search): جمعیتی از راهکارها که دائما در حال بهبود هستند. اگرچه همگرایی در این روش اندکی بیشتر طول می‌کشد، اما معمولا در رسیدگی به مسائل رایج، نتایج بهتری نسبت به مدل‌های جستجو هدایت‌شده به نمایش می‌گذارد.

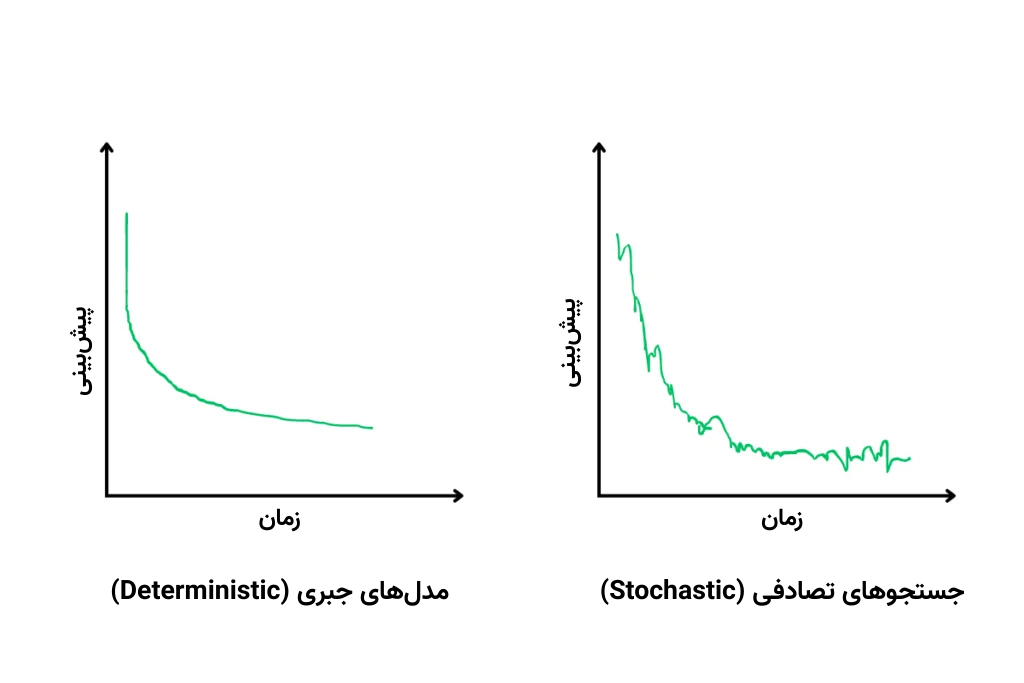
جبری بودن یا تصادفی بودن جستجو

جستجوهای تصادفی یا Stochastic به شکلی تصادفی و اتفاقی به اجرا درمی‌آیند، بنابراین اگر فرایند را دو بار روی داده‌ای یکسان تکرار کنید به نتایج متفاوت می‌رسید. اما مدل‌های جبری یا Deterministic همواره نتایجی یکسان برمی‌گردانند.

الگوریتم ژنتیک الگوریتمی است که از جستجوی جمعیتی و تصادفی کمک می‌گیرد. اما روش کار الگوریتم ژنتیک در پایتون چیست و چرا چنین رویه‌ای را دنبال می‌کند؟

کارکرد الگوریتم ژنتیک

الگوریتم ژنتیک به این خاطر چنین نامی گرفته که رفتار طبیعت را شبیه‌سازی می‌کنند. درست همان‌طور که علت نام‌گذاری شبکه‌های عصبی (Neural Network)، شباهت آن‌ها به نورون‌ها یا عصب‌های موجودات زنده است.

هر یک از کاندیداهای موجود در الگوریتم‌های ژنتیک، «شخص» (Individual) نام دارند. عبارات ژنوتیپ (Genotype)، ژنوم (Genome) یا کروموزوم (Chromosome) هم نشان‌دهنده ساختمان داده در هر شخص هستنند. در این میان، «ژن» (Gene) به هر نقطه‌ای از همان ساختمان داده گفته می‌شود و بلوک‌های داده نیز «آلل» (Allele) نام دارند.

بنابراین کار با مجموعه‌ای از اشخاص شروع می‌شود که هرکدام مقادیر گوناگونی آلل یا داده دارند. البته که تمام اشخاص عملکردی به یک اندازه خوب در بهینه‌سازی هدف ما ندارند (درست همان‌طور که تمام انسان‌ها نمی‌توانند به شکلی برابر با محیط خود تطبیق یابند). در نتیجه، هر شخص که نماینده‌ی یک نمونه از فضای مسئله‌ی واقعی به نام «فنوتیپ» (Phenotype) است توسط تابع ارزیابی یا هدف یا «برازندگی» (Fitness) مورد سنجش قرار می‌گیرد.

برای توضیح باید گفت فنوتیپ به معنی فضا واقعی مساله است که به آن «سنخ‌گونه» هم می‌گویند. برای مثال فرض می‌کنیم که به دنبال طراحی یک میز هستیم. اگر پارامترهای مختلف میز را به صورت ژن در نظر بگیریم، تمام کروموزم‌های بالقوه، فضای Genotype به حساب می‌آیند و تمام فضای صندلی‌های بالقوه هم Phenotype تلقی می‌شوند. تابع برازندگی یا Fitness نیز ارزشی مشخص به هر نقطه از فضا فنوتیپ تخصیص می‌دهد.

فنوتایپ در حقیقت فضای واقعی مسئله هست. مثلا فرض کنیم که می‌خواهیم یک میز طراحی کنیم، اگر پارامترهای مختلف آن را به صورت ژن در نظر بگیریم، تمام کروموزم‌های ممکن فضای genotype می‌شوند و از طرفی کل فضای صندلی‌های ممکن را phenotype می‌گوییم. تابع fitness به هر نقطه از فصای phenotype ارزش متفاوتی می‌دهد.

زمانی که برازندگی هر شخص محاسبه شد، فرایند انتخاب شخص آغاز می‌شود (در ادامه بیشتر به این مورد می‌پردازیم). بنابراین ایده پشت الگوریتم ژنتیک واقعا ساده است: ما به دنبال اشخاصی می‌گردیم که بهترین برازندگی را به نمایش می‌گذارند.

زمانی که انتخاب به پایان می‌رسد، آمیزش اشخاص منتخب به تولید «فرزند» (Offspring) – یا به عبارت دیگر، تولید اشخاص هرچه بیشتر – منتهی می‌شود. به این فرایند «تولید مثل» (Breeding) می‌گویند و تولید اشخاص جدید نیز از طریق عملگرهای ژنتیکی گوناگون مانند «جهش» (Mutation) و «تقاطع» (Crossover) یا «بازترکیب» (Recombination) امکان‌پذیر می‌شود.

بازترکیب به معنای تولید فرزندانی از روی چند والد است و جهش به معنی پدید آوردن تغییر در یکی از اشخاص کنونی.

• برای شروع به سراغ مجموعه‌ای از اشخاص با آلل (مقدار) گوناگون می‌رویم. این اشخاص، جمعیت یا Population الگوریتم ما به حساب می‌آیند.
• اشخاص ارزیابی می‌شوند تا برازندگی هر یک به دست آید.
• سپس حوضچه‌ای از والدین ساخته می‌شود که از آن‌ها برای تولید فرزندان کمک گرفته می‌شود.
• اکنون از روی حوضچه‌ والدین با اعمال عملگرهای بازترکیب و جهش فرزندانی تولید می‌شود و مورد ارزیابی قرار می‌گیرند.
• در گام بعدی این فرزندان با سیاستی در جمعیت جایگزین می‌شوند.
• در نهایت به مرحله دوم بازمی‌گردیم و همین فرایند را با فرزندان تکرار می‌کنیم.

حالا که کارکرد کلی الگوریتم ژنتیک را درک کرده‌اید، می‌توانیم به سراغ آموزش الگوریتم ژنتیک در پایتون برویم. اما پیش از آن فقط باید به دو سوال مهم دیگر نیز پاسخ دهیم: اشخاص چطور انتخاب می‌شوند و تولید اشخاص جدید چطور پیش می‌رود؟

چطور اشخاص را برای تولید فرزند انتخاب کنیم؟

روش‌های گوناگونی برای انتخاب اشخاص در الگوریتم ژنتیک وجود دارد:

• روش چرخ گردان (Roulette Wheel): در این روش ارتباطی مستقیم برازندگی و احتمال انتخاب فرد برای تولید فرزند برقرار می‌شود. در واقع هرچه برازندگی بیشتر باشد، احتمالا انتخاب شدن هم بالاتر می‌رود. برای محاسبه شانس اشخاص، برازندگی آن‌ها بر مجموع برازندگی به دست آمده تقسیم می‌شود.
• رتبه‌بندی (Ranking): اگرچه روش رولت به نظر کاملا معقول جلوه می‌کند، اما اوقاتی که شانس انتخاب اشخاص تقریبا یکسان است به مشکل می‌خورد. در چنین سناریوهایی، ممکن است بهترین شخص ممکن انتخاب نشود. در نتیجه از روش رده‌بندی استفاده می‌کنیم که اشخاص را براساس برازندگی منظم می‌کند و N شخص که بالاترین رتبه را در برازندگی دارند، برگزیده خواهند شد.
• انتخاب تورنمنتی (Tournament-Based Selection): اشخاص به‌صورت گروه گروه در مسابقات شرکت می‌کنند و هربار برنده‌ مسابقه به حوضچه والدین اضافه می‌شود.

چطور اشخاص را در جمعیت جایگزین کنیم؟

• مدل نسلی (Generational): هر بار کل جمعیت با فرزندان تولید شده جایگزین می‌شود.
• مدل حالت استوار (Steady State Selection): در این روش تنها بخشی از جمعیت جایگزین می‌شود. برای مثال یک سیاست نخبه‌سالاری (Elitism) است که در آن بهترین افراد جمعیت حفظ می‌شوند.

تولید اشخاص با تقاطع

به صورت کلی می‌توان به سه روش از تقاطع یا Crossover برای تولید مثل کمک گرفت:

• تقاطع یک‌نقطه‌ای (One-Point Crossing): آلل‌های والدین به دو بخش تقسیم می‌شوند. فرزند این دو، یک بخش آلل را از والد اول و بخش دوم آلل را از والد دوم دریافت می‌کند.
• تقاطع چند نقطه‌ای (Multipoint Crossover): در این روش شاهد ایده‌ای مشابه به مورد قبلی هستیم، اما این بار آلل‌ها به ۳ گروه یا بیشتر تقسیم می‌شوند و فرزندان نیز ترکیبی از این گروه‌ها خواهند بود.
• تقاطع یکپارچه (Uniform Crossing): هر یک از آلل‌های والدین به صورت اتفاقی انتخاب می‌شوند و فرزند آن‌ها نیز ترکیبی اتفاقی از مقادیر والدین خواهد بود.

تولید اشخاص با جهش

وقتی نوبت به جهش می‌رسد، دو روش کلی برای جهش یافتن ژن‌ها داریم:

• جهش تصادفی (Random Mutation): جهش به صورت تصادفی رخ می‌دهد و دربرگیرنده یک آلل (یا یک مقدار) خواهد بود.
• شرینک (Shrink): مقداری تصادفی از توزیعی عادی – یا نوعی دیگر از توزیع‌ها مثل توزیع یکپارچه (Uniform Distribution) – برداشته شده و به مقدار یکی از اشخاص اضافه می‌شود.

حالا که بخش مهمی از دانستنی‌های پیرامون الگوریتم ژنتیک را آموخته‌اید، نوبت به نحوه کار با الگوریتم ژنتیک در پایتون می‌رسد.

کار با الگوریتم ژنتیک در پایتون

برای استفاده از الگوریتم ژنتیک در زبان پایتون به سراغ کتابخانه‌ای به نام PyGAD می‌رویم که ساخت الگوریتم را آسان می‌کند. این کتابخانه انتخابی بسیار محبوب است، زیرا با Keras و PyTorch – دو فریم‌ورک اصلی پایتون برای یادگیری عمیق (Deep Learning) – سازگاری دارد و از انواع تقطیع‌ها، جهش‌ها و انتخاب‌ها پشتیبانی می‌کند.

بنابراین اولین کاری که انجام می‌دهیم، نصب PyGAD است. برای این کار از فرمان زیر استفاده کنید:

pip install pygad

پس از این، می‌خواهیم مساله‌ای نسبتا ساده را حل کنیم: پیدا کردن وزن‌هایی که باید مقادیر گوناگون دریافت کنند تا با ضرب شدن در همان مقادیر، اعدادی مشخص بازگردانند.

برای رسیدگی به این وظیفه از تابع GA در کتابخانه PyGAD استفاده می‌کنیم. این تابع نیاز به تعیین مجموعه‌ای از پارامترها دارد، مثلا دفعات تکرار فرایند، تعداد اشخاصی که جمعیت را تشکیل داده‌اند و همینطور نوع جهش یا تقاطعی که می‌خواهید اتفاق بیفتد.

علاوه بر این باید ارزیابی برازندگی را هم به تابع خاطر نشان کنیم. این تابع به عنوان ورودی، نیاز به یک راهکار (Solution) و گاهی یک فهرست راهکار (Solution Index) دارد و مقدار برازندگی را بازمی‌گرداند.

بیایید نحوه رسیدگی به یک مساله بهینه‌سازی ساده را با PyGAD بررسی کنیم:

import pygad
import numpy

inputs = [0.4,1,0,7,8]
desired_output = 32

def fitness_func(solution, solution_idx):
    output = numpy.sum(solution*inputs)
    fitness = 1.0 / (numpy.abs(output - desired_output) + 0.000001)
    
    return fitness

ga_instance = pygad.GA(num_generations=100,
                       sol_per_pop=10,
                       num_genes=len(inputs),
                       num_parents_mating=2,
                       fitness_func=fitness_func,
                       mutation_type="random",
                       mutation_probability=0.6)

ga_instance.run()

ga_instance.plot_fitness()

همان‌طور که می‌بینیم، برازندگی به دست آمده با مدل ما در ابتدا بسیار پایین بود. اما همینطور که فرایند پیش می‌رود، برازندگی بهبود می‌یابد و بالاخره در نسل ۹۰ به جوابی مطلوب می‌رسد.

دستیابی به راهکار مطلوب نشان می‌دهد که هیچ راهکاری «بهترین» راهکار بالقوه نیست و به همین خاطر هم برازندگی تغییری نکرده است.

حالا بیایید نگاهی به موارد پیچیده‌تر الگوریتم ژنتیک در پایتون بیندازیم.

مسائل بهینه‌سازی با الگوریتم ژنتیک در پایتون

برای درک هرچه بهتر پتانسیل‌های الگوریتم‌های ژنتیک می‌توانیم به سراغ یکی از مسائل کلاسیک در بهینه‌سازی برویم: تعیین مقدار بهینه‌ تولید برای کسب بیشترین سود از محصولات یک شرکت، با توجه به مجموعه‌ای از محدودیت‌ها.

در این مثال، شرکت مورد نظر ما می‌تواند چنین محدودیت‌هایی داشته باشد:

• از هر محصول باید حداقل ۱۰ واحد تولید شود.
• مقدار مواد مصرفی در فرایند تولید محدود است و نمی‌توان از این محدودیت فراتر رفت.
• هر محصول، مزیتی متفاوت به همراه می‌آورد.

برای حل مسائل بهینه‌سازی با الگوریتم ژنتیک در پایتون ابتدا باید تابع را به‌گونه‌ای کدنویسی کنیم که برازندگی یا Fitness را بسنجد. محدودیت‌ها نیز درون تابع محاسبه برازندگی کدنویسی می‌شوند. بنابراین کار را با ساخت چنین تابعی شروع می‌کنیم:

margin = np.array([2, 2.5])
material_consumption = np.array([2,3]) 
material_max = 500

def fitness_func(solution, solution_idx):

  solution_added = solution + 50
  calculated_margin = np.sum(solution_added*margin)
  material_consumed = np.sum(solution_added*material_consumption)
  
  if material_consumed> material_max:
    return 0
  
  else:
    return calculated_margin

# We check a possible solution
print(f"Fitness for correct scenario: {fitness_func(np.array([0, 0]), '')}") 
print(f"Fitness for incorrect scenario: {fitness_func(np.array([0, 1]), '')}") 

Fitness for correct scenario: 225.0
Fitness for incorrect scenario: 227.5

حالا که تابع برازندگی خود را کدنویسی کرده‌ایم، بیایید الگوریتم ژنتیک را به اجرا درآوریم:

ga_instance = pygad.GA(num_generations=1000,
                       sol_per_pop=10,
                       num_genes=2,
                       num_parents_mating=2,
                       fitness_func=fitness_func,
                       mutation_type="random",
                       mutation_probability=0.6
                       )

ga_instance.run()

ga_instance.plot_fitness()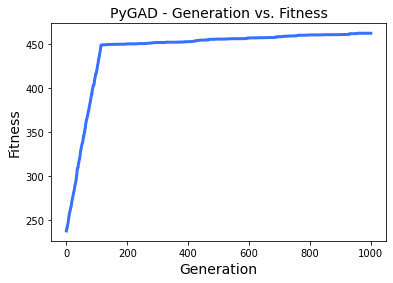

در نهایت نیز می‌توانیم راهکار ارائه‌شده از سوی الگوریتم ژنتیک خود را بررسی کنیم:

ga_instance.best_solution()[0] + 50

array([136.82320846,  75.43757807])

حالا که الگوریتم ژنتیک را درک کرده‌ایم، می‌توانیم در بخش پایانی، پیاده‌سازی کامل الگوریتم ژنتیک را به زبان پایتون یاد بگیریم.

برنامه‌نویسی الگوریتم ژنتیک در پایتون

اگر بخواهیم یک الگوریتم ژنتیک را از نو بسازیم، لازم است:

• جمعیتی حاوی N شخص بسازیم.
• روش‌های مختلف تولید مثل را کدنویسی کنیم.

بنابراین کار را با مورد نخست شروع می‌کنیم: تعریف جمعیت.

ساخت جمعیت برای الگوریتم ژنتیک

برای نوشتن الگوریتم ژنتیک در پایتون از یکی از کلاس‌ها استفاده می‌کنیم و ساخت جمعیت هم در مرحله راه‌اندازی (Initialization) همان کلاس انجام می‌شود. با این حال برای اینکه همگرایی به شکلی سریع‌تر و آسان‌تر انجام شود، جمعیت را به دو شکل می‌سازیم:

• راه‌اندازی تصادفی آلل‌ها: خیلی ساده مقادیری تصادفی تولید می‌شوند که نیاز به بهینه‌سازی دارند. این نوع از راه‌اندازی زمانی انجام می‌شود که پارامتر gene_limits صفر باشد.
• راه‌اندازی محدود آلل‌ها: روی هر یک از آلل‌های ما محدودیت‌های گوناگون اعمل می‌شود. بنابراین مقادیر به شکلی تصادفی، اما مطابق با محدودیت‌ها تولید خواهند. زمانی که پارامتر gene_limits صفر نباشد، این نوع راه‌اندازی اتفاق می‌افتد.

با اطلاعات بالا، کد راه‌اندازی تصادفی جمعیت چنین شمایلی دارد:

import numpy as np


class GeneticAlgorithm:
  def __init__(self, n_variables, n_genes, random_state = None, gene_limits = None):

    self.n_variables = n_variables
    self.n_genes = n_genes
    self.gene_limits = gene_limits 
    self.random_state = random_state
    
    # Create the population
    if self.gene_limits is not None:
      
      # Check that both vectors have the same length
      assert len(self.gene_limits) == self.n_variables

      limits = [np.random.uniform(limit[0], limit[1], self.n_genes)
        for limit in self.gene_limits] 

    else:
      limits = [np.random.random(self.n_genes)
        for limit in range(self.n_variables)]
      
    # Convert list of limits to list of solutions
    self.population = list(zip(*limits))
        
ga = GeneticAlgorithm(
    n_variables = 2,
    n_genes = 10
)

ga.population

[(0.3248594341550495, 0.7747988337644331),
 (0.9641753689879542, 0.2728028066671938),
 (0.7745274418319132, 0.2833543446404905),
 (0.8258487102100652, 0.9961554551162345),
 (0.034136970844815595, 0.7000431609346188),
 (0.9956365394402079, 0.6007170537947054),
 (0.5622396252894827, 0.6793736336026693),
 (0.16433824493155325, 0.579682515374066),
 (0.15570018999931567, 0.46125127275801037),
 (0.5544543502640932, 0.8094380724657084)]

حالا که جمعیت داریم، می‌توانیم به مرحله بعد و به سراغ محاسبه برازندگی برویم.

محاسبه برازندگی در الگوریتم ژنتیک

وقتی کار با جمعیت شروع می‌شود، باید به الگوریتم ژنتیک خود اجازه دهیم یک تابع برازندگی دریافت کند. از این تابع برای محاسبه برازندگی هر یک از راهکارها به صورت داخلی استفاده می‌کنیم.

بنابراین کد بخش قبلی را گسترش می‌دهیم و پارامتر جدید fitness_func را اضافه می‌کنیم که یک راه حل به عنوان ورودی دریافت می‌کند و مقدار برازندگی یا Fitness Value را بازمی‌گرداند.

علاوه بر این، متدی به نام get_fitness_scores هم می‌سازیم که نمره برازندگی راهکار کنونی را بازمی‌گرداند. به این ترتیب استفاده از امتیاز برازندگی در سراسر الگوریتم آسان‌تر می‌شود.

حالا بیایید کد را گسترش دهیم تا حاوی برازندگی باشد:

import numpy as np
import inspect

class GeneticAlgorithm:
  def __init__(
      self, n_variables, n_genes, mutation_type = 'random', random_state = None, 
      gene_limits = None, fitness_func = None):

    assert mutation_type in ['random']

    self.n_variables = n_variables
    self.n_genes = n_genes
    self.gene_limits = gene_limits 
    self.mutation_type = mutation_type
    self.random_state = random_state
    self.fitness_func = fitness_func
 
    # Create the population
    if self.gene_limits is not None:
      
      # Check that both vectors have the same length
      assert len(self.gene_limits) == self.n_variables

      limits = [np.random.uniform(limit[0], limit[1], self.n_genes)
        for limit in self.gene_limits] 

    else:
      limits = [np.random.random(self.n_genes)
        for limit in range(self.n_variables)]
      
    # Convert list of limits to list of solutions
    self.population = list(zip(*limits))
  
  def get_fitness_scores(self):
    scores = [self.fitness_func(ind) for ind in self.population]
    return np.array(scores)

def fitness_func(solution):
  solution = np.array(solution)
  solution_added = solution + 50
  calculated_margin = np.sum(solution_added*margin)
  material_consumed = np.sum(solution_added*material_consumption)
  
  if material_consumed> material_max:
    return 0
  
  else:
    return calculated_margin

ga = GeneticAlgorithm(
    n_variables = 2,
    n_genes = 10,
    fitness_func= fitness_func
)

fitness_scores = ga.get_fitness_scores()
fitness_scores

array([228.53122328, 227.3974419 , 226.11156266, 227.45136065,
       225.92371642, 226.86141269, 228.93654237, 228.35770696,
       226.48405291, 227.82272666])

حالا که می‌توانیم تمام اشخاص حاضر در جمعیت را ارزیابی کنیم، به فاز بعدی کار می‌رویم: انتخاب اشخاص توسط الگوریتم ژنتیک در پایتون.

برنامه‌نویسی انتخاب اشخاص

زمانی که امکان ارزیابی با تابع مهیا می‌شود، می‌توانیم سیستم انتخاب بهترین نامزدها را بسازیم. سیستمی که در ادامه می‌سازیم اجازه می‌دهد فرایند انتخاب را به دو شکل پیش ببریم: روش رده‌بندی و روش تورنمنت.

در روش رده‌بندی، خیلی ساده باید به دنبال شاخص‌هایی باشیم که از نظر برازندگی، بهترین نتیجه را به نمایش می‌گذارند. همان‌طور که می‌توان در کد دید، پارامتری جدید به الگوریتم اضافه می‌شود که تعداد اشخاص منتخب برای تولید مثل را نشان می‌دهد.

برای روش تورنمنت هم بیشترین جفت‌های تصادفی ممکن را از ژن‌های مورد نظر خود در جمعیت می‌سازیم و بالاترین مقدار را از هر جفت انتخاب می‌کنیم.

بیایید کدهای سیستم انتخاب خود را ببینیم:

def ranking_selection(scores, k):
    if k is None:
      raise ValueError('K must not be none if type ranking is selected.')
    
    ind = np.argpartition(scores, k)[-k:]

    return ind

def tournament_selection(scores, k, n_candidates):
  candidates = [np.random.randint(0, len(scores), 3) for i in range(3)]
  tournament_winner = [np.argmax(scores[tournament]) for i, tournament in enumerate(candidates)]
  ind = [tournament[tournament_winner[i]] for i, tournament in enumerate(candidates)]

  return np.array(ind)

def gene_selection(scores, type, k, n_candidates = None):

  if type not in ['ranking','tournament']:
    raise ValueError('Type should be ranking or tournament')
  
  if type == 'ranking':
    ind = ranking_selection(scores, k)
  elif type == 'tournament':
    ind = tournament_selection(scores, k, n_candidates)
  else:
    pass

  return ind


ranking_selection = gene_selection(scores= fitness_scores,
               type = 'ranking',
               k = 3
               )

tournament_selection = gene_selection(scores= fitness_scores,
               type = 'tournament',
               k = 3,
               n_candidates = 11
               )

print(f"""
Ranking selection results: {ranking_selection}
Tournament selection results: {tournament_selection}
""")

Ranking selection results: [7 6 0]
Tournament selection results: [7 0 6]

حالا که سیستم انتخاب هم ساخته شده، سیستم «تولید» (Generation) را هم برای نسل‌های جدید می‌سازیم.

کدنویسی تولید مثل

برای اینکه تولید نسل‌های جدید امکان‌پذیر شود، باید به مدل خود اجازه دهیم که هم از تقاطع و هم جهش کمک بگیرد. در نتیجه پارامتر دیگری (transformation_type) هم خواهیم داشت که نشان‌دهنده نوع دگرگونی است.

از نظر تقاطع ها نیز امکان استفاده از دو نوع تقاطع را مهیا می کنیم: تقاطع یکپارچه و تقاطع تک‌نقطه‌ای.

در هر دو حالت لازم است در نظر داشته باشیم که دو فرزند جدید از دو والد به دست می‌آیند. در نتیجه، تعداد جفت‌هایی که تولید می‌شوند باید نصف تعداد تمام اشخاص در جمعیت باشد:

def crossover(parent1, parent2, crossover_type):

  # Check crossover type
  if crossover_type not in ['uniform', 'one_point']:
    raise ValueError('crossover_type should be one of uniform, one_point or multi_point')
  
  if crossover_type == 'one_point':
    index = np.random.choice(range(len(parent1)))
    children = [parent2[:index] + parent1[index:], parent1[:index] + parent2[index:]]

  elif crossover_type == 'uniform':
    parents = list(zip(*[parent1,parent2]))
    children1 = tuple([np.random.choice(element) for element in parents])
    children2 = tuple([np.random.choice(element) for element in parents])
    children = [children1, children2]
  else:
    pass

  return children

children_uniform = crossover(
    ga.population[0],
    ga.population[1],
    crossover_type = 'uniform'
    )

children_onepoint = crossover(
    ga.population[0],
    ga.population[1],
    crossover_type = 'one_point'
    )

print(f"""
Children Uniform: {children_uniform}
Children One Point: {children_onepoint}
""")

Children Uniform: [(0.8750958900239486, 0.6664701872724336), (0.8750958900239486, 0.7124125982046803)]
Children One Point: [(0.8750958900239486, 0.7124125982046803), (0.36563321798453374, 0.6664701872724336)]

حالا که تقاطع الگوریتم ژنتیک در پایتون را برنامه‌نویسی کرده‌ایم، نوبت به کدنویسی جهش می‌رسد. همان‌طور که پیش‌تر نیز اشاره کردیم، به صورت کلی دو نوع جهش داریم:

• رشته بیت (Bit String): تغییراتی تصادفی در یکی از آلل‌ها به وجود می‌آورد.
• شرینک (Shrink): یکی از مقادیر موجود در یک توزیع نرمال را به یکی از آلل‌ها اضافه می‌کند.

در این رویه، نتایجی متفاوت نسبت به تقاطع خواهیم داشت، زیرا درحالی که تقاطع دو فرزند با خود به همراه می‌آورد، در جهش تنها شاهد تولید یک فرزند هستیم.

def mutation(individual, mutation_type):

  if mutation_type not in ['bitstring', 'shrink']:
    raise ValueError('mutation_type should be one of bitstring or shrinkg')
  
  # Get index of individual to modify
  index = np.random.choice(len(individual))

  # Convert individual to list so that can be modified
  individual_mod = list(individual)

  if mutation_type == 'bitstring':      
    individual_mod[index] = 1 - individual_mod[index]
  
  else:
    individual_mod[index] = individual_mod[index] + np.random.rand()
  
  # Convert indivudal to tuple
  individual = tuple(individual_mod)

  return individual

mutation_bitstring = mutation(ga.population[0], mutation_type = 'bitstring')
mutation_shrink = mutation(ga.population[0], mutation_type = 'shrink')


print(f"""
Mutation bitstring: {mutation_bitstring}
Mutation shrink: {mutation_shrink}
""")

با اضافه شدن کد بالا، به تمام مواد لازم برای الگوریتم ژنتیک خود دسترسی پیدا کرده‌ایم. در نهایت نوبت به این می‌رسد که تمام بلوک‌های کد را کنار هم بگذاریم و الگوریتم ژنتیک در پایتون را بسازیم.

برنامه‌نویسی تکامل در الگوریتم ژنتیک

برای اینکه تکامل (Evolution) را در الگوریتم خود پیاده کنیم، لازم است خیلی ساده بلوک‌های کد پیشین را کنار هم بگذاریم و برای این کار از متد Optimize کمک می‌گیریم.

برای نهایی کردن الگوریتم خود، چند سوال به‌خصوص – مانند مقدار Best_Fitness_Evolution – تعیین کرده‌آیم که نتایج بهترین برازندگی در هر نسل را پایش می‌کنند.

به صورت مشابه، متدی دیگر به نام view_fitness_evolution نیز ساخته‌ایم که تکامل بهترین برازندگی به دست آمده را مصورسازی می‌کند، درست مانند آنچه پیش‌تر با PyGAD دیدیم.

بنابراین کد نهایی الگوریتم ژنتیک ما در پایتون به شکل زیر خواهد بود:

import numpy as np
import inspect
from tqdm import tqdm
import matplotlib.pyplot as plt

class GeneticAlgorithm:
  def __init__(
      self,
      n_variables,
      n_genes,
      n_iterations,
      transformation_type = None,
      mutation_type = None,
      crossover_type = None,
      gene_selection_type = None,
      n_selected_individuals = None,
      n_candidates = None,
      random_state = None, 
      gene_limits = None,
      fitness_func = None
      ):

    # Make validations
    if transformation_type not in ['mutation', 'transformation']:
      raise ValueError('transformation_type should be one of mutation or transformation.')

    self.n_variables = n_variables
    self.n_genes = n_genes
    self.gene_limits = gene_limits 
    self.transformation_type = transformation_type
    self.mutation_type = mutation_type
    self.random_state = random_state
    self.fitness_func = fitness_func
    self.n_iterations = n_iterations
    self.gene_selection_type = gene_selection_type
    self.n_selected_individuals = n_selected_individuals
    self.n_candidates = n_candidates
    self.crossover_type = crossover_type
    self.best_fitness_evolution = []

    # Asserts 
    # Check that fitness function is a function
    assert callable(fitness_func)
 
    # Create the population
    if self.gene_limits is not None:
      
      # Check that both vectors have the same length
      assert len(self.gene_limits) == self.n_variables

      limits = [np.random.uniform(limit[0], limit[1], self.n_genes)
        for limit in self.gene_limits] 

    else:
      limits = [np.random.random(self.n_genes)
        for limit in range(self.n_variables)]
      
    # Convert list of limits to list of solutions
    self.population = np.array(list(zip(*limits)))

  def get_fitness_scores(self):
    scores = [self.fitness_func(ind) for ind in self.population]
    scores = np.array(scores)
    return scores 

  def __append_best_score(self, scores):
    best_score = np.max(scores)
    self.best_fitness_evolution.append(best_score)
    return 'Ok'


  def __ranking_selection(self, k):
      if k is None:
        raise ValueError('K must not be none if type ranking is selected.')
      
      ind = np.argpartition(self.get_fitness_scores(), k)[-k:]
      return ind

  def __tournament_selection(self, k, n_candidates):
    candidates = [np.random.randint(0, len(self.get_fitness_scores()), 3) for i in range(3)]
    tournament_winner = [np.argmax(self.get_fitness_scores()[tournament]) for i, tournament in enumerate(candidates)]
    ind = [tournament[tournament_winner[i]] for i, tournament in enumerate(candidates)]

    return np.array(ind)

  def gene_selection(self, gene_selection_type, k, n_candidates = None):

    if gene_selection_type not in ['ranking','tournament']:
      raise ValueError('Type should be ranking or tournament')
    
    if gene_selection_type == 'ranking':
      ind = self.__ranking_selection(k)
    elif gene_selection_type == 'tournament':
      ind = self.__tournament_selection(k, n_candidates)
    else:
      pass

    return ind
  
  def __crossover(self, parent1, parent2, crossover_type):
    
    # Check crossover type
    if crossover_type not in ['uniform', 'one_point']:
      raise ValueError('crossover_type should be one of uniform, one_point or multi_point')
    
    if crossover_type == 'one_point':
      index = np.random.choice(range(len(parent1)))
      children = parent2[:index] + parent1[index:], parent1[:index] + parent2[index:]

    elif crossover_type == 'uniform':
      parents = list(zip(*[parent1,parent2]))
      children1 = tuple([np.random.choice(element) for element in parents])
      children2 = tuple([np.random.choice(element) for element in parents])
      children = children1, children2
    else:
      pass

    return children


  def __mutation(self, individual, mutation_type):

    if mutation_type not in ['bitstring', 'shrink']:
      raise ValueError('mutation_type should be one of bitstring or shrinkg')
    
    # Get index of individual to modify
    index = np.random.choice(len(individual))

    # Convert individual to list so that can be modified
    individual_mod = list(individual)

    if mutation_type == 'bitstring':      
      individual_mod[index] = 1 - individual_mod[index]
    
    else:
      individual_mod[index] = individual_mod[index] + np.random.rand()
    
    # Convert indivudal to tuple
    individual = tuple(individual_mod)

    return individual

  def optimize(self):
    
    for i in tqdm(range(self.n_iterations)):

      # Calculate fitness score
      scores = self.get_fitness_scores()

      # Append best score
      _ = self.__append_best_score(scores)

      # Make Selection
      selected_genes = self.gene_selection(
          gene_selection_type = self.gene_selection_type,
          k = self.n_selected_individuals,
          n_candidates = self.n_candidates
          )
      
      # Get selected population
      selected_population = self.population[selected_genes.tolist()]
      

      # Make transformations (mutation/crossover)
      if self.transformation_type == 'mutation':
        transformed_genes_index = np.random.choice(
            range(len(selected_population)),
            self.n_genes
            )
        

        new_population = [self.__mutation(selected_population[i], self.mutation_type)
          for i in transformed_genes_index]
      
      else:
        # Get pairs of parents
        parents_pairs = np.random.choice(
            selected_genes,
            (int(self.n_genes/2),2)
            )
        
        # For each pair, make crossover
        new_population = [self.__crossover(self.population[parents[0]],
                                           self.population[parents[1]],
                                           crossover_type=self.crossover_type
                                           )
          for parents in parents_pairs]
        
        # Unnest population
        new_population = [child for children in new_population for child in children]
      
      # Set new population as population
      self.population = np.array(new_population)
    
    # When n_iterations are finished, fitness score
    scores = self.get_fitness_scores()

    # Append best score
    _ = self.__append_best_score(scores)

    # Get the result where the result is the best
    best_score_ind =np.argpartition(scores, 0)[0]
    
    best_solution = self.population[best_score_ind]

    return (best_solution, self.best_fitness_evolution[-1])

  def view_fitness_evolution(self):
    plt.plot(
        range(len(self.best_fitness_evolution)),
        self.best_fitness_evolution
    )

در نهایت لازم است کد خود را تست و با سنجش جهش و تقاطع، نتایج بازگشتی هرکدام را بررسی کنیم. اول به سراغ جهش می‌رویم:

ga = GeneticAlgorithm(
  n_variables = 2,
  n_genes = 10,
  n_iterations = 50,
  transformation_type = 'mutation', #transformation
  mutation_type = 'shrink',
  #crossover_type = 'uniform',
  gene_selection_type = 'ranking',
  n_selected_individuals = 3,
  #n_candidates = None,
  #random_state = None, 
  #gene_limits = None,
  fitness_func = fitness_func
  )

print(ga.optimize())
ga.view_fitness_evolution()

بعد هم تقاطع را پیاده‌سازی می‌کنیم:

ga = GeneticAlgorithm(
  n_variables = 2,
  n_genes = 10,
  n_iterations = 50,
  transformation_type = 'transformation',
  crossover_type = 'uniform',
  gene_selection_type = 'ranking',
  n_selected_individuals = 3,
  fitness_func = fitness_func
  )

print(ga.optimize())
ga.view_fitness_evolution()

100%|██████████| 50/50 [00:00<00:00, 693.67it/s]
(array([0.97573885, 0.93485633]), 229.28861852920954)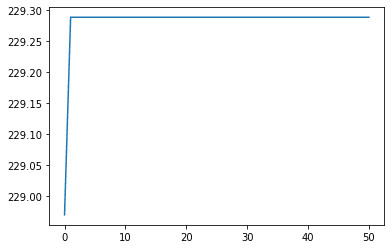

همان‌طور که می‌توان دید، مدل ما هنگام کار با هر دو روش به خوبی کار می‌کند و برازندگی را با از راه رسیدن هر نسل جدیدی، بهبود می‌بخشد.

جمع‌بندی الگوریتم ژنتیک در پایتون

به عنوان جمع‌بندی باید گفت که بدون هیچ تردید، الگوریتم‌های ژنتیک کاربرد فراوان در مدل‌های بهینه‌سازی دارند و تمام دیتا ساینتیست‌ها باید این الگوریتم‌ها را بشناسند. در این مطلب نحوه کار این الگوریتم‌ها و همینطور پیاده‌سازی الگوریتم ژنتیک در پایتون را آموختیم و می‌توانید از مهارت جدیدتان در مدل‌های بهینه‌سازی و مدل‌های هایپرپارامتر (Hyperparameter) کمک بگیرید.

منبع: Ander Fernandez